
已知函数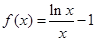 .
.
(1)试判断函数 的单调性;
的单调性;
(2)设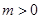 ,求
,求 在
在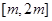 上的最大值;
上的最大值;
(3)试证明:对任意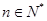 ,不等式
,不等式 都成立(其中
都成立(其中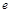 是自然对数的底数).
是自然对数的底数).
(1)函数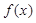 在
在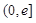 上单调递增,在
上单调递增,在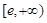 上单调递减;
上单调递减;
(2) 在
在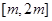 上的最大值为
上的最大值为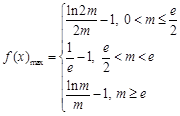 ;
;
(3)证明过程详见试题解析.
解析试题分析:(1)先对函数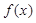 求导,令导函数为0,即可求得函数在
求导,令导函数为0,即可求得函数在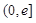 上单调递增,在
上单调递增,在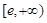 上单调递减. (2)结合函数的单调性,分
上单调递减. (2)结合函数的单调性,分 时,
时,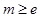 时,
时,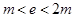 三种情况进行讨论,即可求
三种情况进行讨论,即可求 在
在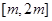 上的最大值;(3) 把证明过程转化为恒成立问题即可.
上的最大值;(3) 把证明过程转化为恒成立问题即可.
试题解析:(1)解:(1)函数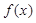 的定义域是
的定义域是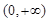 .由已知
.由已知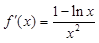 .令
.令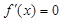 ,得
,得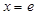 .
.
因为当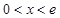 时,
时,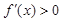 ;当
;当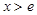 时,
时,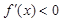 .
.
所以函数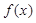 在
在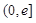 上单调递增,在
上单调递增,在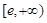 上单调递减.
上单调递减.
(2)由(1)可知当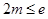 ,即
,即 时,
时,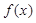 在
在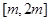 上单调递增,所以
上单调递增,所以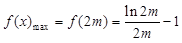 .
.
当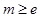 时,
时,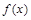 在
在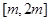 上单调递减,所以
上单调递减,所以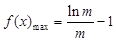 .当
.当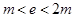 ,即
,即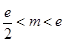 时,
时,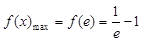 .综上所述,
.综上所述,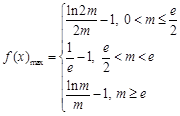
(3)由(1)知当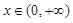 时
时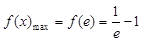 .所以在
.所以在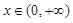 时恒有
时恒有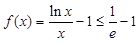 ,即
,即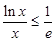 ,当且仅当
,当且仅当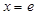 时等号成立.因此对任意
时等号成立.因此对任意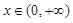 恒有
恒有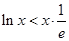 .因为
.因为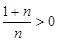 ,
,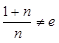 ,所以
,所以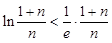 ,即
,即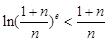 .因此对任意
.因此对任意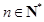 ,不等式
,不等式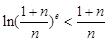 .
.
考点:导函数的应用、最值问题、恒成立问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
据环保部门测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比,比例常数为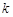
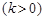 .现已知相距18
.现已知相距18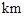 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为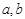 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数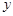 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设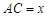 (
(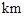 ).
).
(1)试将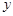 表示为
表示为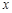 的函数; (2)若
的函数; (2)若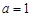 ,且
,且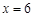 时,
时,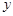 取得最小值,试求
取得最小值,试求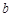 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点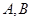 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;
(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.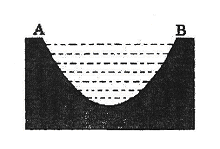
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线 y = x3 + x-2 在点 P0 处的切线 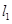 平行于直线
平行于直线
4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线 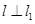 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, .
.
(1)若曲线 在点
在点 处的切线平行于
处的切线平行于 轴,求
轴,求 的值;
的值;
(2)当 时,若对
时,若对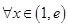 ,
,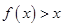 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)设 ,在(1)的条件下,证明当
,在(1)的条件下,证明当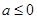 时,对任意两个不相等的正数
时,对任意两个不相等的正数 、
、 ,有
,有 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com