
已知函数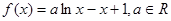 .
.
(1)求 的单调区间;
的单调区间;
(2)若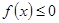 在
在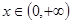 上恒成立,求所有实数
上恒成立,求所有实数 的值;
的值;
(3)对任意的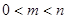 ,证明:
,证明: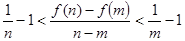
(1)当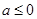 时,
时,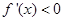 ,
, 减区间为
减区间为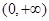 ;当
;当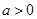 时,
时, 递增区间为
递增区间为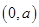 ,递减区间为
,递减区间为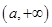 ;(2)
;(2)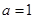 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)利用导数判断函数的单调性,就是在定义域内考虑 导函数的符号,先求导函数得,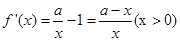 ,令
,令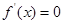 ,得
,得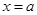 ,讨论根与定义域的关系,当
,讨论根与定义域的关系,当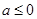 时,
时,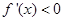 ,
, 减区间为
减区间为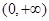 ;当
;当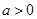 时,将定义域分段,分别考虑导函数的符号,即得函数的单调区间;(1)只需函数
时,将定义域分段,分别考虑导函数的符号,即得函数的单调区间;(1)只需函数 的最大值小于等于0即可,由(1)得,当
的最大值小于等于0即可,由(1)得,当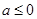 时,
时, 减区间为
减区间为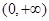 ,且
,且 ,故不满足;当
,故不满足;当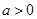 时,
时,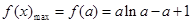 ,记
,记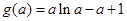 ,可求得
,可求得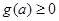 ,故
,故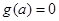 ,故
,故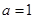 ;(3)由(2)得,当且仅当
;(3)由(2)得,当且仅当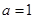 时,
时,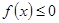 恒成立,即
恒成立,即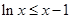 ,又
,又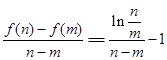 ,结合起来证明即可.
,结合起来证明即可.
试题解析:(1)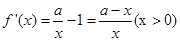 , 1分
, 1分
当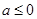 时,
时,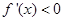 ,
, 减区间为
减区间为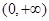 2分
2分
当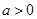 时,由
时,由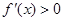 得
得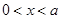 ,由
,由 得
得 3分
3分
∴ 递增区间为
递增区间为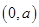 ,递减区间为
,递减区间为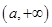 4分
4分
(2)由(1)知:当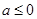 时,
时, 在
在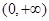 上为减区间,而
上为减区间,而
∴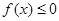 在区间
在区间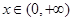 上不可能恒成立 5分
上不可能恒成立 5分
当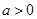 时,
时, 在
在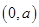 上递增,在
上递增,在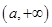 上递减,
上递减,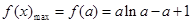 ,令
,令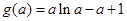 , 6分
, 6分
依题意有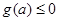 ,而
,而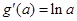 ,且
,且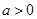
∴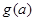 在
在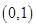 上递减,在
上递减,在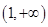 上递增,
上递增,
∴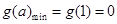 ,故
,故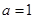 9分
9分
(3)由(2)知: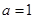 时,
时,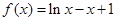 且
且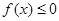 恒成立
恒成立
即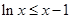 恒成立
恒成立
则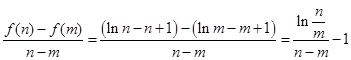
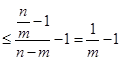 11分
11分
又由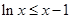


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=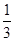 x3-ax+1.
x3-ax+1.
(1)求x=1时,f(x)取得极值,求a的值;
(2)求f(x)在[0,1]上的最小值;
(3)若对任意m∈R,直线y=-x+m都不是曲线y=f(x)的切线,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司经销某种产品,每件产品的成本为6元,预计当每件产品的售价为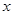 元(
元(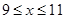 )时,一年的销售量为
)时,一年的销售量为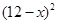 万件。
万件。
(1)求公司一年的利润y(万元)与每件产品的售价x的函数关系;
(2)当每件产品的售价为多少时,公司的一年的利润y最大,求出y最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂有一批货物由海上从甲地运往乙地,已知轮船的最大航行速度为60海里/小时,甲地至乙地之间的海上航行距离为600海里,每小时的运输成本由燃料费和其他费用组成,轮船每小时的燃料费与轮船速度的平方成正比,比例系数为0.5,其余费用为每小时1250元。
(1)把全程运输成本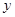 (元)表示为速度
(元)表示为速度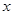 (海里/小时)的函数;
(海里/小时)的函数;
(2)为使全程运输成本最小,轮船应以多大速度行驶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com