
据环保部门测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比,比例常数为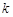
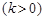 .现已知相距18
.现已知相距18 的A,B两家化工厂(污染源)的污染强度分别为
的A,B两家化工厂(污染源)的污染强度分别为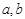 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数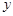 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设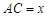 (
(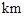 ).
).
(1)试将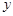 表示为
表示为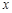 的函数; (2)若
的函数; (2)若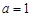 ,且
,且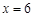 时,
时,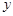 取得最小值,试求
取得最小值,试求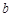 的值.
的值.
(1) 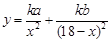 , (2) 8.
, (2) 8.
解析试题分析:(1)解实际问题应用题,关键要正确理解题意,正确列出等量关系,注意考虑函数定义域. 设点C受A污染源污染程度为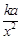 ,点C受B污染源污染程度为
,点C受B污染源污染程度为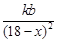 ,其中
,其中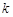 为比例系数,且
为比例系数,且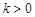 .从而点C处受污染程度
.从而点C处受污染程度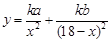 .定义域为
.定义域为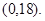 (2) 因为
(2) 因为 ,所以,
,所以,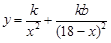 ,求复杂分式函数最值,通常考虑利用导数求解.
,求复杂分式函数最值,通常考虑利用导数求解. 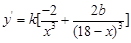 ,令
,令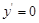 ,得
,得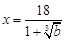 ,因此函数在
,因此函数在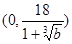 单调减,在
单调减,在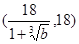 单调增,即在
单调增,即在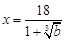 时函数取极小值,也是最小值. 又此时
时函数取极小值,也是最小值. 又此时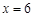 ,解得
,解得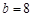 ,经验证符合题意.
,经验证符合题意.
解:(1)设点C受A污染源污染程度为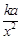 ,点C受B污染源污染程度为
,点C受B污染源污染程度为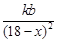 ,其中
,其中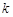 为比例系数,且
为比例系数,且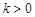 . 4分
. 4分
从而点C处受污染程度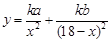 . 6分
. 6分
(2)因为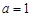 ,所以,
,所以,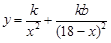 , 8分
, 8分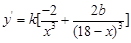 ,令
,令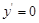 ,得
,得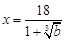 , 12分
, 12分
又此时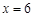 ,解得
,解得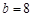 ,经验证符合题意.
,经验证符合题意.
所以,污染源B的污染强度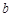 的值为8. 14分
的值为8. 14分
考点:利用导数求函数值域


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数 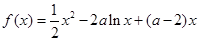 ,
,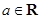 .
.
(1)当 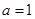 时,求函数
时,求函数 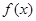 的最小值;
的最小值;
(2)当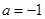 时,求证:无论
时,求证:无论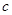 取何值,直线
取何值,直线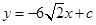 均不可能与函数
均不可能与函数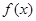 相切;
相切;
(3)是否存在实数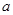 ,对任意的
,对任意的 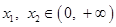 ,且
,且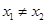 ,有
,有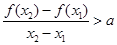 恒成立,若存在求出
恒成立,若存在求出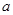 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•浙江)已知a∈R,函数f(x)=2x3﹣3(a+1)x2+6ax
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若|a|>1,求f(x)在闭区间[0,|2a|]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=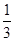 x3-ax+1.
x3-ax+1.
(1)求x=1时,f(x)取得极值,求a的值;
(2)求f(x)在[0,1]上的最小值;
(3)若对任意m∈R,直线y=-x+m都不是曲线y=f(x)的切线,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数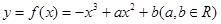
(1)若函数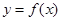 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;
(2)设函数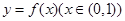 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求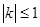 的充要条件;
的充要条件;
(3)若函数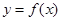 的图象上任意不同的两点的连线的斜率小于l,求证
的图象上任意不同的两点的连线的斜率小于l,求证 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com