二次函数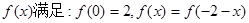
，它的导函数的图象与直线
平行.
（1）求
的解析式；
（2）若函数
的图象与直线
有三个公共点，求m的取值范围．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：解答题
某工厂有一批货物由海上从甲地运往乙地，已知轮船的最大航行速度为60海里/小时，甲地至乙地之间的海上航行距离为600海里，每小时的运输成本由燃料费和其他费用组成，轮船每小时的燃料费与轮船速度的平方成正比，比例系数为0.5，其余费用为每小时1250元。
(1)把全程运输成本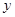
（元）表示为速度
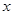（海里/小时）的函数；
(2)为使全程运输成本最小，轮船应以多大速度行驶？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
(
,
为自然对数的底数).
(1)若曲线
在点
处的切线平行于
轴,求
的值;
(2)求函数
的极值;
(3)当
的值时,若直线
与曲线没有公共点,求
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
一个圆柱形圆木的底面半径为1m，长为10m，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形
（如图所示，其中O为圆心，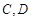
在半圆上），设
，木梁的体积为V（单位：m3），表面积为S（单位：m2）．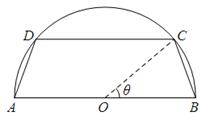
（1）求V关于θ的函数表达式；
（2）求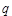
的值，使体积V最大；
（3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
设函数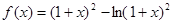
，
（1）求函数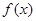
的单调区间；
（2）若当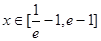
时，不等式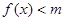
恒成立，求实数
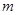的取值范围；
（3）若关于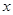
的方程
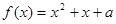在区间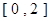
上恰好有两个相异的实根，求实数
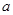的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）
．
，根据
求出
，然后根据
可得对称轴，导函数图象与直线
平行可求出
，从而求出函数的解析式；（1 1 ）先利用导数求出函数的极值，然后根据函数
的图象与直线
有三个公共点，可知
的取值范围应介于两极值之间．
，所以
．
，所以图像的对称轴
．
从而解得：
，
．
，
．
则有
或
在
、
上递增，
上递减 ，且
．
的单调区间；
恰有两个交点，求
的取值范围．
.
的单调性；
，求
上的最大值；
，不等式
都成立（其中
是自然对数的底数）．
在(0，1)上单调递减．
，求
在[1，2]上的最小值．
是
的导函数，
，且函数
.
的表达式；
的单调区间和极值.