练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的中心在原点，焦点在轴，焦距为2，且长轴长是短轴长的倍．

    （1）求椭圆的标准方程；

    （2）设，过椭圆左焦点的直线交于、两点，若对满足条件的任意直线，不等式（）恒成立，求的最小值．

    【答案】（1）（2）的最小值为

    【解析】

    试题分析：（1）依题意，求出，，可得椭圆的标准方程；（2）设，，可得，首先讨论当直线垂直于轴时， ．

    当直线不垂直于轴时，设直线：，与椭圆方程联立，得到

    ，，则，将

    及，代入可得，要使不等式（）恒成立，只需，即的最小值为．

    试题解析：（1）依题意，，，

    解得，，∴椭圆的标准方程为．

    （2）设，，所以，

    当直线垂直于轴时，，且，此时，，

    所以．

    当直线不垂直于轴时，设直线：，

    由整理得，

    所以，，

    所以

    ．

    要使不等式（）恒成立，只需，即的最小值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知关于的一次函数.

    （1）设集合和，分别从集合和中随机取一个数作为和，求函数是增函数的概率；

    （2）实数满足条件，求函数的图象经过第一、二、三象限的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】衡州市英才中学贯彻党的教育方针，促进学生全面发展，积极组织开展了丰富多样的社团活动，根据调查，英才中学在传统民族文化的继承方面开设了“泥塑”、“剪纸”、“曲艺”三个社团，三个社团参加的人数如下表所示：

    社团

    泥塑

    剪纸

    曲艺

    人数

    320

    240

    200

    为调查社团开展情况，学校社团管理部采用分层抽样的方法从中抽取一个容量为的样本，已知从“剪纸”社团抽取的同学比从“泥塑”社团抽取的同学少2人。

    （1）求三个社团分别抽取了多少同学；

    （2）若从“剪纸”社团抽取的同学中选出2人担任该社团活动监督的职务，已知“剪纸”社团被抽取的同学中有2名女生，求至少有1名女同学被选为监督职务的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某单位员工的月工资水平，从该单位500位员工中随机抽取了50位进行调查，得到如下频数分布表和频率分布直方图：

    月工资

    （单位：百元）

    [15,25)

    [25,35)

    [35,45)

    [45,55)

    [55,65)

    [65,75)

    男员工数

    1

    8

    10

    6

    4

    4

    女员工数

    4

    2

    5

    4

    1

    1

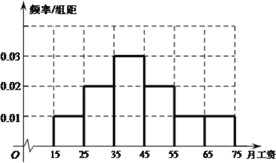
    (1) 试由上图估计该单位员工月平均工资；

    (2)现用分层抽样的方法从月工资在和的两组所调查的男员工中随机选取5人，问各应抽取多少人？

    (3)若从月工资在和两组所调查的女员工中随机选取2人，试求这2人月工资差不超过1000元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】海关对同时从，，三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如下表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．

    地区

    数量

    50

    150

    100

    （1）求这6件样品中来自，，各地区商品的数量；

    （2）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数.

    （1）当时，求在区间上的最值；

    （2）讨论的单调性；

    （3）当时，有恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，直线经过点A (1，0).

    （1）若直线与圆C相切，求直线的方程；

    （2）若直线与圆C相交于P，Q两点，求三角形CPQ面积的最大值，并求此时直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设直线l的方程为(a＋1)x＋y＋2－a＝0(a∈R)．

    （1）若l在两坐标轴上的截距相等，求l的方程；

    （2）若l不经过第二象限，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前项和为，且，N*

    （1）求数列的通项公式；

    （2）已知（N*），记（且），是否存在这样的常数，使得数列是常数列，若存在，求出的值；若不存在，请说明理由．

    （3）若数列，对于任意的正整数，均有

    成立，求证：数列是等差数列．

    查看答案和解析>>

    同步练习册答案