【题目】已知平面多边形
中，
，
，
，
，
，
为
的中点，现将三角形
沿
折起，使
.
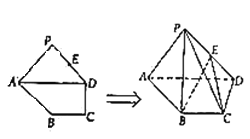
（1）证明：
平面
；
（2）求三棱锥
的体积.
【答案】（1）详见解析；（2）
.
【解析】
（1）取
的中点
，连
，即可证明
，结合
即可证明四边形
为平行四边形，问题得证。
（2）取
中点
，连接
，
，先说明
平面
，即可求得三角形为等边三角形，取的中点
，先说明
平面
，利用体积变换及中点关系，将
转化成
，问题得解。
解：（1）取的中点，连.
∵
为
中点，∴为
的中位线，
∴.
又，∴
，
∴四边形为平行四边形，∴
.
∵
平面
，
平面，
∴
平面.
（2）由题意知
为等腰直角三角形，为直角梯形.
取中点，连接，，
∵
，∴
，
∵
，
，
，∴
平面，
∴平面，∵
平面，∴
.
∴在直角三角形
中，
，
，∴
，
∴三角形为等边三角形.
取的中点，则
，
，
，
∴平面，
，
∵为的中点，∴到平面的距离等于
到平面的距离的一半，
∴
.
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，如图所示，已知椭圆
的左、右顶点分别为
，
，右焦点为
.设过点
的直线
，
与此椭圆分别交于点
，
，其中
，
，
.
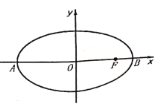
（1）设动点
满足：
，求点的轨迹；
（2）设
，
，求点
的坐标；
（3）设
，求证：直线
必过
轴上的一定点（其坐标与
无关），并求出该定点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2018年10月28日，重庆公交车坠江事件震惊全国，也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.
社区委员会针对居民的学习结果进行了相关的问卷调查，并将得到的分数整理成如图所示的统计图.
（Ⅰ）求得分在
上的频率；
（Ⅱ）求社区居民问卷调查的平均得分的估计值；（同一组中的数据以这组数据所在区间中点的值作代表）
（Ⅲ）以频率估计概率，若在全部参与学习的居民中随机抽取5人参加问卷调查，记得分在
间的人数为
，求的分布列.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如上图所示，在正方体
中， 
分别是棱
的中点， 
的顶点
在棱
与棱
上运动，有以下四个命题：
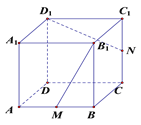
A．平面
； B．平面
⊥平面
；
C． 
在底面
上的射影图形的面积为定值；
D． 
在侧面
上的射影图形是三角形．其中正确命题的序号是__________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列四个结论：
①命题“
，
”的否定是“
，
”；
②命题“若
，则
且
”的否定是“若，则
”；
③命题“若
，则或”的否命题是“若，则
或
”；
④若“
是假命题，
是真命题”，则命题
，
一真一假.
其中正确结论的个数为（ ）
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某旅游爱好者计划从3个亚洲国家A1，A2，A3和3个欧洲国家B1，B2，B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个，求这2个国家都是亚洲国家的概率；
(2)若从亚洲国家和欧洲国家中各选1个，求这两个国家包括A1，但不包括B1的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
