练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如上图所示，在正方体中， 分别是棱的中点， 的顶点在棱与棱上运动，有以下四个命题：

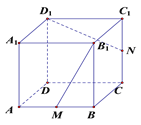
    A．平面 ； B．平面⊥平面；

    C． 在底面上的射影图形的面积为定值；

    D． 在侧面上的射影图形是三角形．其中正确命题的序号是__________.

    【答案】

    【解析】由正方体的几何性质对4个命题进行判断，对于A，当动点P与点重合时， 以等腰三角形， 与不垂直，所以不能得出平面，A为假命题；对于B，易证，所以平面，所以平面⊥平面，故B为真命题；对于C， 在底面上的射影图形的面积为定值，因为在底面的射影是三角形，底边是，点P在底面的射影在CD上，到的距离不变，若正方体棱长为时，则射影面积为为定值，所以C为真命题；对于D，当P点与点重合时，则点与点P的投影重合，此时 在侧面上的射影图形是线段，不是三角形，故D是假命题。真命题有BC.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某人在微信群中发了一个8元“拼手气”红包，被甲、乙、丙三人抢完，若三人均领到整数元，且每人至少领到1元，则甲领到的钱数不少于其他任何人的概率为

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知设函数.

    （1）若，求极值；

    （2）证明：当，时，函数在上存在零点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题:函数在定义域上单调递增；命题:在区间上恒成立.

    （1）如果命题为真命题，求实数的值或取值范围;

    （2）命题“”为真命题,“”为假命题，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面多边形中，，，，，，为的中点，现将三角形沿折起，使.

    （1）证明：平面；

    （2）求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求函数的单调区间；

    （2）解关于的不等式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图①，在五边形中，，，，，将沿折起到的位置，得到如图②所示的四棱锥，为线段的中点，且平面.

    （1）求证：平面.

    （2）若直线与所成角的正切值为，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于的方程恰有3个实数根，，，则__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四面体中，，平面平面，，且.

    （1）证明：平面；

    （2）设为棱的中点，当四面体的体积取得最大值时，求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案