
【题目】如图①,在五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,得到如图②所示的四棱锥
的位置,得到如图②所示的四棱锥![]() ,
,![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() .
.
(2)若直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,又
,又![]() 为
为![]() 的中点,得到四边形
的中点,得到四边形![]() 为平行四边形,从而应用线面平行的判定定理证得结果.
为平行四边形,从而应用线面平行的判定定理证得结果.
(2)![]() ,可得
,可得![]() 为直线
为直线![]() 与
与![]() 所成的角,可得
所成的角,可得![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,取
,取![]() 的中点O,连接PO,过O作AB的平行线,可建立如图所示的空间直角坐标系O-xyz,设
的中点O,连接PO,过O作AB的平行线,可建立如图所示的空间直角坐标系O-xyz,设![]() 为平面PBD的法向量,则
为平面PBD的法向量,则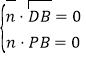 ,利用
,利用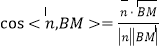 ,即可得出.
,即可得出.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() .
.
又![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
则四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解:因为![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() .
.
由![]() ,即
,即![]() 及
及![]() 为
为![]() 的中点,可得
的中点,可得![]() 为等边三角形,所以
为等边三角形,所以![]() .
.
又![]() ,所以
,所以![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
因为![]() ,所以
,所以![]() 即为直线
即为直线![]() 与
与![]() 所成的角,
所成的角,
所以![]() ,所以
,所以![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向,建立空间直角坐标系,如图所示.
轴的正方向,建立空间直角坐标系,如图所示.
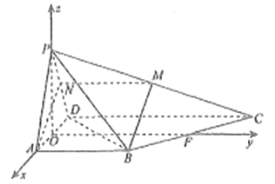
则![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则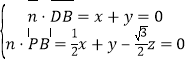 ,
,
令![]() ,则
,则![]() .
.
因为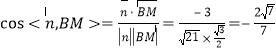 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】
某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温![]() (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程![]() .
.
(参考公式: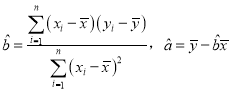 .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年10月28日,重庆公交车坠江事件震惊全国,也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.![]() 社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.
社区委员会针对居民的学习结果进行了相关的问卷调查,并将得到的分数整理成如图所示的统计图.

(Ⅰ)求得分在![]() 上的频率;
上的频率;
(Ⅱ)求![]() 社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
社区居民问卷调查的平均得分的估计值;(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)以频率估计概率,若在全部参与学习的居民中随机抽取5人参加问卷调查,记得分在![]() 间的人数为
间的人数为![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
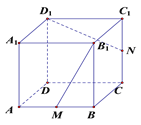
【题目】如上图所示,在正方体![]() 中,
中, ![]() 分别是棱
分别是棱![]() 的中点,
的中点, ![]() 的顶点
的顶点![]() 在棱
在棱![]() 与棱
与棱![]() 上运动,有以下四个命题:
上运动,有以下四个命题:
A.平面![]()
![]() ; B.平面
; B.平面![]() ⊥平面
⊥平面![]() ;
;
C. ![]()
![]() 在底面
在底面![]() 上的射影图形的面积为定值;
上的射影图形的面积为定值;
D. ![]()
![]() 在侧面
在侧面![]() 上的射影图形是三角形.其中正确命题的序号是__________.
上的射影图形是三角形.其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
①命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
②命题“若![]() ,则
,则![]() 且
且![]() ”的否定是“若
”的否定是“若![]() ,则
,则![]() ”;
”;
③命题“若![]() ,则
,则![]() 或
或![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() 或
或![]() ”;
”;
④若“![]() 是假命题,
是假命题,![]() 是真命题”,则命题
是真命题”,则命题![]() ,
,![]() 一真一假.
一真一假.
其中正确结论的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且过点P
,且过点P![]() 。
。
(1)求椭圆的标准方程;
(2)已知斜率为1的直线l过椭圆的右焦点F交椭圆于A.B两点,求弦AB的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点在抛物线
的左焦点在抛物线![]() 的准线上,且椭圆的短轴长为2,
的准线上,且椭圆的短轴长为2,![]() 分别为椭圆的左,右焦点,
分别为椭圆的左,右焦点,![]() 分别为椭圆的左,右顶点,设点
分别为椭圆的左,右顶点,设点![]() 在第一象限,且
在第一象限,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求
的面积,求![]() 的值;
的值;
(Ⅲ)设点![]() 为
为![]() 的中点,射线
的中点,射线![]() (
(![]() 为原点)与椭圆交于点
为原点)与椭圆交于点![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某公园内有两条道路![]() ,
,![]() ,现计划在
,现计划在![]() 上选择一点
上选择一点![]() ,新建道路
,新建道路![]() ,并把
,并把![]() 所在的区域改造成绿化区域.已知
所在的区域改造成绿化区域.已知![]() ,
,![]()
![]() .
.
(1)若绿化区域![]() 的面积为1
的面积为1![]() ,求道路
,求道路![]() 的长度;
的长度;
(2)若绿化区域![]() 改造成本为10万元/
改造成本为10万元/![]() ,新建道路
,新建道路![]() 成本为10万元/
成本为10万元/![]() .设
.设![]() (
(![]() ),当
),当![]() 为何值时,该计划所需总费用最小?
为何值时,该计划所需总费用最小?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com