
【题目】
某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温![]() (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程![]() .
.
(参考公式: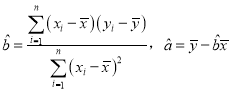 .)
.)
【答案】(1)![]() (2)
(2)![]()
【解析】
试题(1)利用列举法写出抽出2组数据的所有基本事件,并从中找出2组数据恰好是相邻2天数据的基本事件,利用古典概型公式求出概率;(2)先求出![]() 和
和![]() ,再利用参考公式算出
,再利用参考公式算出![]() 和
和![]() ,代入即可得线性回归方程.
,代入即可得线性回归方程.
试题解析:(1)解:设“选取的2组数据恰好是相邻2天数据”为事件![]() .
.
所有基本事件(m,n)(其中m,n为1月份的日期数)有:(11,12),(11,13),(11,14),
(11,15),(12,13),(12,14),(12,15),(13,14),(13,15),(14,15)共10种.
事件![]() 包括的基本事件有(11,12),(12,13),(13,14),(14,15)共4种.
包括的基本事件有(11,12),(12,13),(13,14),(14,15)共4种.
∴![]() .
.
(2)解:由数据,求得![]() ,
,![]() .
.
![]()
![]() ,
,
∴ y关于x的线性回归方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】以下说法错误的是( )
A.复数![]() 满足
满足![]() ,则复数
,则复数![]() 在复平面上对应的点的轨迹为直线.
在复平面上对应的点的轨迹为直线.
B.![]() 为
为![]() 上连续可导的函数,若
上连续可导的函数,若![]() ,则
,则![]() 为极值点.
为极值点.
C.若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
D.![]() 为抛物线
为抛物线![]() 的两点,
的两点,![]() 为坐标原点,若
为坐标原点,若![]() ,则直线
,则直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
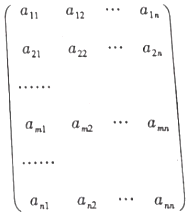
【题目】在如图所示的数阵中每一行从左到右均是首项为1,项数为n的等差数列,设第![]() 行的等差数列中的第k项为
行的等差数列中的第k项为![]() 2,3,
2,3,![]() ,
,![]() ,公差为
,公差为![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 也成等差数列.
也成等差数列.
![]() Ⅰ
Ⅰ![]() 求
求![]() ;
;
![]() Ⅱ
Ⅱ![]() 求
求![]() 关于m的表达式;
关于m的表达式;
![]() Ⅲ
Ⅲ![]() 若数阵中第i行所有数之和
若数阵中第i行所有数之和![]() ,第j列所有数之和为
,第j列所有数之和为![]() ,是否存在i,j满足
,是否存在i,j满足![]() ,使得
,使得![]() 成立?若存在,请求出i,j的一组值;若不存在,请说明理由.
成立?若存在,请求出i,j的一组值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在微信群中发了一个8元“拼手气”红包,被甲、乙、丙三人抢完,若三人均领到整数元,且每人至少领到1元,则甲领到的钱数不少于其他任何人的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,离心率等于
的中心在坐标原点,离心率等于![]() ,它的一个长轴端点恰好是抛物线
,它的一个长轴端点恰好是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 、
、![]() (
(![]() )是椭圆上的两点,
)是椭圆上的两点,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,且直线
两侧的动点,且直线![]() 的斜率为
的斜率为![]() .
.
①求四边形APBQ的面积的最大值;
②求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成![]() ,
,![]() 两组,每组20人,
两组,每组20人,![]() 组群众给第一阶段的创文工作评分,
组群众给第一阶段的创文工作评分,![]() 组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图所示的茎叶图.
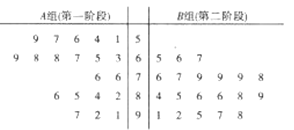
(Ⅰ)根据茎叶图比较群众对两个阶段的创文工作满意度评分的平均值和集中程度(不要求计算出具体值,给出结论即可);
(Ⅱ)完成下面的列联表,并通过计算判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | 合计 | |
第一阶段 | |||
第二阶段 | |||
合计 |
参考公式:![]() ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2014·长春模拟)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图.
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、方差,并判断选谁参加比赛更合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,得到如图②所示的四棱锥
的位置,得到如图②所示的四棱锥![]() ,
,![]() 为线段
为线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() .
.
(2)若直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com