
【题目】一矩形的一边在![]() 轴上,另两个顶点在函数
轴上,另两个顶点在函数![]() 的图像上,如图,则此矩形绕
的图像上,如图,则此矩形绕![]() 轴旋转而成的几何体的体积的最大值是( )
轴旋转而成的几何体的体积的最大值是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
用![]() 表示圆柱的体积可得
表示圆柱的体积可得![]() ,由基本不等式可求其最大值,从而得到正确的选项.
,由基本不等式可求其最大值,从而得到正确的选项.
因为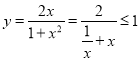 当且仅当
当且仅当![]() 时取等号,所以
时取等号,所以![]() .
.
因为矩形绕![]() 轴旋转一周旋转得到一个圆柱,
轴旋转一周旋转得到一个圆柱,
设![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,
则圆柱的底面圆的半径为![]() ,高为
,高为![]() ,
,
因为![]() ,即
,即![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以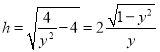 ,
,
所以圆柱得体积为![]() ,
,
当且仅当![]() 时取等号,
时取等号,
所以矩形绕![]() 轴旋转而成的几何体的体积的最大值是
轴旋转而成的几何体的体积的最大值是![]() ,
,
故选:A.
【点晴】
本题主要考查了空间几何体的体积的计算、基本不等式的应用,解答的关键确定![]() 的值,属于中档试题,同时着重考查了转化与化归的思想方法及数形结合的思想方法的应用,本题的解答中先求出
的值,属于中档试题,同时着重考查了转化与化归的思想方法及数形结合的思想方法的应用,本题的解答中先求出![]() 的范围,再设出点
的范围,再设出点![]() 的坐标,根据
的坐标,根据![]() 两点的纵坐标相等得到
两点的纵坐标相等得到![]() ,再求出高
,再求出高![]() ,根据图形旋转得到一个圆柱,根据圆柱的体积公式得到关系式,利用基本不等式求最值.
,根据图形旋转得到一个圆柱,根据圆柱的体积公式得到关系式,利用基本不等式求最值.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=nan+n,数列{bn}的前n项和为Tn,求满足不等式![]() 的n的最小值.
的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
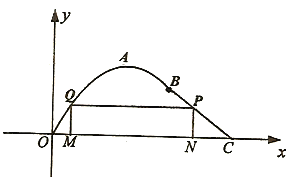
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有5道题,其中3道甲类题![]() ,2道乙类题
,2道乙类题![]() 。
。
(1)若从这5道题中任选2道,求这2道题至少有1道题是乙类题的概率;
(2)若从甲类题、乙类题中各选1道题,求这2道题包括![]() 但不包括
但不包括![]() 的概率。
的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有学生1000名,经调查,其中750名同学经常参加体育锻炼(称为![]() 类同学),另外250名同学不经常参加体育锻炼(称为
类同学),另外250名同学不经常参加体育锻炼(称为![]() 类同学),现用分层抽样方法(按
类同学),现用分层抽样方法(按![]() 类、
类、![]() 类分两层)从该年级的学生中共抽取100名同学,如果以身高达
类分两层)从该年级的学生中共抽取100名同学,如果以身高达![]() 作为达标的标准,对抽取的100名学生,得到以下列联表:
作为达标的标准,对抽取的100名学生,得到以下列联表:
身高达标 | 身高不达标 | 总计 | |
经常参加体育锻炼 | 40 | ||
不经常参加体育锻炼 | 15 | ||
总计 | 100 |
(Ⅰ)完成上表;
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为经常参加体育锻炼与身高达标有关系(![]() 的观测值精确到0.001)?
的观测值精确到0.001)?
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() ,
,![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差平方和越小的模型,拟合的效果越好;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点;
至少经过其样本数据点中的一个点;
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强.
之间的负相关很强.
以上正确说法的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;>300为严重污染.一环保人士记录了某地2020年某月10天的AQI的茎叶图如图所示.
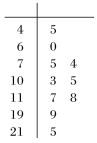
(1)利用该样本估计该地本月空气质量优良(AQI≤100)的天数;(按这个月总共有30天计算)
(2)若从样本中的空气质量不佳(AQI>100)的这些天中,随机地抽取两天深入分析各种污染指标,求该两天的空气质量等级恰好不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一矩形钢板ABCD缺损了一角(如图所示),边缘线OM上每一点到点D的距离都等于它到边AB的距离.工人师傅要将缺损的一角切割下来使剩余部分成一个五边形,若AB=1m,AD=0.5m,则五边形ABCEF的面积最大值为____m2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com