
分析 (1)由零点分段法进行分类讨论,可以解得f(x)≤x+2的解集;
(2)将不等式f(x)≤log2(a2-4a+12)对任意实数a恒成立的条件转化为f(x)≤3,代入即可得出a的取值范围.
解答 解:(1)由f(x)≤x+2得|x+1|+|x-1|≤x+2
∵$\left\{{\begin{array}{l}{x≤-1}\\{1-x-(x+1)≤x+2}\end{array}}\right.$或$\left\{{\begin{array}{l}{-1<x<1}\\{1-x+x+1≤x+2}\end{array}}\right.$或$\left\{\begin{array}{l}{x≥1}\\{x-1+x+1≤x+2}\end{array}\right.$…3 分
解得0≤x≤2…4 分
∴f(x)≤x+2的解集为{x|0≤x≤2}…6 分
(2)∵a2-4a+12=(a-2)2+8≥8,∴${log_2}({a^2}-4a+12)≥3$…8 分
故$f(x)≤{log_2}({a^2}-4a+12)$恒成立等价于f(x)≤3…(9分)
即|x+1|+|x-1|≤3,易得$-\frac{3}{2}≤x≤\frac{3}{2}$…(11分)
∴x的范围是$\{x|-\frac{3}{2}≤x≤\frac{3}{2}\}$…12 分
点评 本题考查绝对值不等式的求解方法,考查学生灵活转化问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$$\overrightarrow{AC}$+$\frac{1}{6}$$\overrightarrow{BD}$ | B. | $\frac{1}{6}$$\overrightarrow{AC}$+$\frac{5}{6}$$\overrightarrow{BD}$ | C. | -$\frac{5}{6}$$\overrightarrow{AC}$+$\frac{1}{6}$$\overrightarrow{BD}$ | D. | $\frac{5}{6}$$\overrightarrow{AC}$-$\frac{1}{6}$$\overrightarrow{BD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 和$\frac{1}{2}$ | B. | 15和$\frac{1}{4}$ | C. | 18和$\frac{2}{3}$ | D. | 20和$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n=4,p=0.6 | B. | n=6,p=0.4 | C. | n=8,p=0.3 | D. | n=24,p=0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
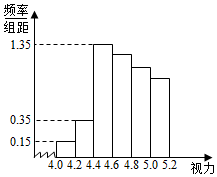 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.| 年级名次 是否近视 | 前50名 | 后50名 |
| 近视 | 42 | 34 |
| 不近视 | 8 | 16 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,6] | B. | (1,6) | C. | {1,2,3,4} | D. | {2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com