
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如下茎叶图所示:

(1)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2) 从乙的5次培训成绩中随机选择2个,试求选到121分的概率.
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源:2014高考名师推荐数学理科三角函数图象变换(解析版) 题型:选择题
已知函数f(x)=Acos(ωx+ )(A>0,ω>0,
)(A>0,ω>0, ?R),则“f(x)是奇函数”是“
?R),则“f(x)是奇函数”是“ =
= ”的( )
”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
某学校餐厅新推出 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
| 满意 | 一般 | 不满意 |
A套餐 | 50% | 25% | 25% |
B套餐 | 80% | 0 | 20% |
C套餐 | 50% | 50% | 0 |
D套餐 | 40% | 20% | 40% |
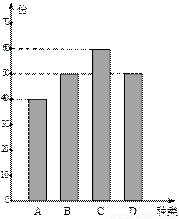
(1)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(2)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
给定抛物线 ,
,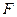 是抛物线
是抛物线 的焦点,过点
的焦点,过点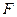 的直线
的直线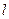 与
与 相交于
相交于 、
、 两点,
两点, 为坐标原点.
为坐标原点.
(1)设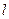 的斜率为1,求以
的斜率为1,求以 为直径的圆的方程;
为直径的圆的方程;
(2)设 ,求直线
,求直线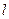 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).

查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科预测题(解析版) 题型:解答题
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
API |
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为ω。在区间[0,100]对企业没有造成经济损失;在区间 对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
(1)试写出是S(ω)的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
|
附:

| 非重度污染 | 重度污染 | 合计 |
供暖季 |
|
|
|
非供暖季 |
|
|
|
合计 |
|
| 100 |
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科选择题专项训练(解析版) 题型:选择题
在△ABC中,角A,B,C所对的边分别为a,b,c.若acosA=bsinB,则sinAcosA+cos2B=( )
A. B.
B. C.-1 D.1
C.-1 D.1
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科解答题前三题(解析版) 题型:解答题
已知向量a=(cosωx,sinωx),b=(cosωx, cosωx),其中0<ω<2,函数
cosωx),其中0<ω<2,函数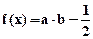 ,其图象的一条对称轴为
,其图象的一条对称轴为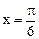 。
。
(1)求函数的表达式及单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,S△ABC为其面积,若 ,b=1,
,b=1, ,求a的值。
,求a的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com