
己知等比数列 所有项均为正数,首
所有项均为正数,首 ,且
,且 成等差数列.
成等差数列.
(I)求数列 的通项公式;
的通项公式;
(II)数列 的前n项和为
的前n项和为 ,若
,若 ,求实数
,求实数 的值.
的值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
【解析】(Ⅰ)设出等比数列 的公比为
的公比为 ,则由等比数列的通项公式可用q的式子将
,则由等比数列的通项公式可用q的式子将 分别表示出来,再由
分别表示出来,再由 成等差数列,由等差数列的性质可得
成等差数列,由等差数列的性质可得 从而可得到关于q的方程,解此方程可得q的值,再注意到等比数列
从而可得到关于q的方程,解此方程可得q的值,再注意到等比数列 所有项均为正数,所以q>0,从而可写出数列
所有项均为正数,所以q>0,从而可写出数列 的通项公式;(Ⅱ)先记
的通项公式;(Ⅱ)先记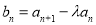 ,则
,则 知当
知当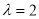 时不符合题意,当
时不符合题意,当 时,数列
时,数列 为等比数列,利用等比数列的前n项和公式用
为等比数列,利用等比数列的前n项和公式用 表示出其前n项和,结合已知条件即可得
表示出其前n项和,结合已知条件即可得 的值.
的值.
试题分析:(Ⅰ)设等比数列 的公比为
的公比为 ,由条件得
,由条件得 成等差数列,所以
成等差数列,所以 ,
,
解得 ; 由数列
; 由数列 的所有项均为正数,则
的所有项均为正数,则 =2
=2
数列 的通项公式为
的通项公式为

(Ⅱ)记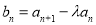 ,则
,则
若 不符合条件;
不符合条件;
若 , 则
, 则 ,数列
,数列 为等比数列,首项为
为等比数列,首项为 ,公比为2,
,公比为2,
此时 又
又 ,所以
,所以
考点:1.等差数列的性质;2.等比数列的性质;3.数列的求和.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源:2015届山西省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,并计算出 ,则下列说法正确的( )
,则下列说法正确的( )
A.这种疫苗能起到预防甲型H1N1流感的有效率为1%
B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1
C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”
D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”
查看答案和解析>>
科目:高中数学 来源:2015届山西省高二3月月考文科数学试卷(解析版) 题型:选择题
在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当
 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的 =20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )
=20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )
A.有95%的把握认为两者有关 B.约有95%的打鼾者患心脏病
C.有99%的把握认为两者有关 D.约有99%的打鼾者患心脏病
查看答案和解析>>
科目:高中数学 来源:2015届山东省高二暑假作业数学试卷五(解析版) 题型:选择题
下列四个判断:
① ;
;
②已知随机变量X服从正态分布N(3, ),P(X≤6)=0.72,则P(X≤0)=0.28;
),P(X≤6)=0.72,则P(X≤0)=0.28;
③已知 的展开式的各项系数和为32,则展开式中x项的系数为20;
的展开式的各项系数和为32,则展开式中x项的系数为20;
④
其中正确的个数有:
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com