
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 在数集的扩展过程中,有些性质是可以传递的,但有些性质不能传递,因此,要判断类比的结果是否正确,关键是要在新的数集里进行论证,当然要想证明一个结论是错误的,也可直接举一个反例,要想得到本题的正确答案,可对4个结论逐一进行分析,不难解答.
解答 解:①若a,b∈C,当a=1+i,b=i时,a-b=1>0,但a,b 是两个虚数,不能比较大小.故①错误
②“若a,b∈R,则a•b∈R”类比推出“若a,b∈C,则a•b∈C″,正确;
③由向量$\overrightarrow a$的性质|$\overrightarrow a$|2=${\overrightarrow a^2}$,类比复数z的性质|z|2=z2;两者属性不同一个是数,一个是即有大小又有方向的量,不具有类比性,故错误;
④在有理数集Q中,若a+b$\sqrt{2}$=c+d$\sqrt{2}$⇒(a-c)+$\sqrt{2}$(b-d)=0⇒a=c,b=d”,正确;
故选:B.
点评 本题考查类比推理,解题的关键掌握并理解类比推理的定义,并能根据类比的定义鉴别所举的事例是否满足类比推理.


科目:高中数学 来源: 题型:解答题
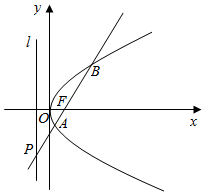 已知抛物线C:y2=2px(p>0),其焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线于P点.
已知抛物线C:y2=2px(p>0),其焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线于P点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在三棱锥P-ABC中,AB=BC=$\sqrt{6}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=$\sqrt{3}$
如图所示,在三棱锥P-ABC中,AB=BC=$\sqrt{6}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=$\sqrt{3}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {3,5} | C. | {5} | D. | {1,2,3,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com