考点:命题的真假判断与应用
专题:证明题,空间位置关系与距离
分析:利用面面平行的判定定理与性质定理,面面垂直的判定定理与三棱锥体积轮换公式对①②③④四个选项逐一分析判断即可.
解答:
解:①,在正方体ABCD-A
1B
1C
1D
1中,D
1A∥C
1B,D
1A?平面A
1BC
1,C
1B?平面A
1BC
1,
∴D
1A∥平面A
1BC
1,
同理可证,D
1C∥平面A
1BC
1,D
1A∩D
1C=D
1,
∴平面D
1AC∥平面A
1BC
1,又D
1P?平面D
1AC,
∴D
1P∥平面A
1BC
1,故①正确;
②,当点P为AC与BD的交点时,BD⊥平面BDD
1,D
1P?平面BDD
1,这时,D
1P⊥BD,除此之外,D
1P不与BD垂直,故②错误;
③,∵DB
1在平面A
1B
1C
1D
1上的射影为B
1D
1,B
1D
1⊥A
1C
1(正方形的两条对角线互相垂直),
DB
1在平面BB
1C
1C的射影为B
1C,B
1C⊥BC
1(正方形的两条对角线互相垂直),
由三垂线定理的逆定理可知,B
1D⊥A
1C
1,B
1D⊥BC
1,A
1C
1∩BC
1=C
1,
∴B
1D⊥平面A
1BC
1,B
1D?平面PDB
1,
∴平面PDB
1⊥平面A
1BC
1,故③正确;
④,设正方体的边长为1,点B到平面A
1BC
1的距离就是点B到平面A
1ACC
1的距离,为
BD=
,
S△A1PC1=
A
1C
1•h=
×
×1=
,
∵
VA1-BPC1=
VB-A1PC1=
S△A1PC1•
BD=
×
()2=
,为定值,故④正确.
故答案为:①③④.
点评:本题考查空间直线与平面、平面与平面的位置关系及体积,突出考查面面平行的判定定理与性质定理,考查面面垂直的判定定理,考查几何体的体积运算,属于难题.

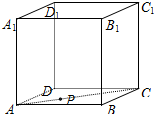 如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题:
如图,在正方体ABCD-A1B1C1D1中,点P在面对角线AC上运动,给出下列命题:

 通城学典默写能手系列答案
通城学典默写能手系列答案