练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    求矩阵M=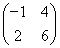的特征值和特征向量.

     

    当t≠0时,属于λ1=7的特征向量为

    当t≠0时,所以属于λ2=-2的特征向量为

    【解析】特征多项式λ2-5λ-14=(λ-7)(λ+2),

    由(λ-7)(λ+2)=0可得:λ1=7,λ2=-2.

    由可得2x-y=0,

    ∴(x,y)=(t,2t).

    当t≠0时,属于λ1=7的特征向量为,

    由可得x+4y=0,

    ∴(x,y)=(4t,-t),

    当t≠0时,所以属于λ2=-2的特征向量为.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷（解析版） 题型：选择题

    设等比数列{an}的各项均为正数,公比为q,前n项和为Sn.若对?n∈N*,有S2n<3Sn,则q的取值范围是(　　)

    (A)(0,1](B)(0,2)(C)[1,2)(D)(0,)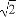

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷（解析版） 题型：解答题

    某校举行环保知识大奖赛,比赛分初赛和决赛两部分.初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题连续两次答错的概率为.(已知甲回答每个问题的正确率相同,并且相互之间没有影响.)

    (1)求选手甲回答一个问题的正确率.

    (2)求选手甲可进入决赛的概率.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十四选修4-2第一节练习卷（解析版） 题型：解答题

    已知2×2矩阵M=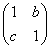,矩阵M对应的变换将点(2,1)变换成点(4,-1),求矩阵M将圆x2+y2=1变换后的曲线方程.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十六选修4-2第三节练习卷（解析版） 题型：解答题

    对任意实数x,矩阵总存在特征向量,求m的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷（解析版） 题型：解答题

    求直线(t为参数)被圆(α为参数)截得的弦长.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十五选修4-2第二节练习卷（解析版） 题型：解答题

    已知△ABC,A(-1,0),B(3,0),C(2,1),对它先作关于x轴的反射变换,再将所得图形绕原点逆时针旋转90°.

    (1)分别求两次变换所对应的矩阵M1,M2.

    (2)求△ABC在两次连续的变换作用下所得到的△A'B'C'的面积.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷（解析版） 题型：填空题

    抛掷两枚骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功次数X的期望是　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷（解析版） 题型：解答题

    现有甲、乙两个靶,某射手向甲靶射击一次,命中的概率为,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立,假设该射手完成以上三次射击.

    (1)求该射手恰好命中一次的概率.

    (2)求该射手的总得分X的分布列.

     

    查看答案和解析>>

    同步练习册答案