
分析 (Ⅰ)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(Ⅱ)当a>0时,求得f(ax)-af(x)=|ax-1|-|a-ax|,利用绝对值不等式的性质可得|ax-1|-|a-ax|≤|ax-1+a-ax|=f(a),从而可证结论.
解答 解:(Ⅰ)函数f(x)=|x-1|,不等式:f(x)+f(x-1)≤2,即|x-1|+|x-2|≤2,
∴$\left\{\begin{array}{l}{x<1}\\{1-x+2-x≤2}\end{array}\right.$①,或$\left\{\begin{array}{l}{1≤x≤2}\\{x-1+(2-x)≤2}\end{array}\right.$②,或 $\left\{\begin{array}{l}{x>2}\\{x-1+x-2≤2}\end{array}\right.$③,
解①求得$\frac{1}{2}$≤x<1,解②求得 1≤x≤2,解③求得2<x≤$\frac{5}{2}$.
综合可得,不等式的解集为{x|$\frac{1}{2}$≤x≤$\frac{5}{2}$}.
(Ⅱ)证明:若a>0,则f(ax)-af(x)=|ax-1|-a|x-1|=|ax-1|-|ax-a|≤|(ax-1)-(ax-a)|=|a-1|=f(a),
即f(ax)-af(x)≤f(a)成立.
点评 本题主要考查绝对值不等式的解法,掌握双绝对值不等式的性质,通过分类讨论去掉绝对值符号是解题的关键,考查转化思想与分类讨论思想的综合应用,属于中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
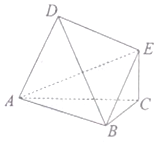 如图△ABC和△ABD均为等腰直角三角形,AD⊥BD,AC⊥BC,平面ABC⊥平面ABD,EC⊥平面ABC,EC=1,$AD=2\sqrt{2}$.
如图△ABC和△ABD均为等腰直角三角形,AD⊥BD,AC⊥BC,平面ABC⊥平面ABD,EC⊥平面ABC,EC=1,$AD=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -3 | C. | -$\frac{7}{5}$ | D. | -$\frac{11}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,6) | B. | (-1,6) | C. | (-2,1) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 正次品 | 甲正品 甲正品 乙正品 | 甲正品 甲正品 乙次品 | 甲正品 甲次品 乙正品 | 甲正品 甲次品 乙次品 | 甲次品 甲次品 乙正品 | 甲次品 甲次品 乙次品 |
| 频 数 | 15 | 20 | 16 | 31 | 10 | 8 |
| 正次品 | 乙正品 乙正品 甲正品 | 乙正品 乙正品 甲次品 | 乙正品 乙次品 甲正品 | 乙正品 乙次品 甲次品 | 乙次品 乙次品 甲正品 | 乙次品 乙次品 甲次品 |
| 频 数 | 8 | 10 | 20 | 22 | 20 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢游泳 | 不喜欢游泳 | 合计 | |
| 男生 | 10 | ||
| 女生 | 20 | ||
| 合计 |
| p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
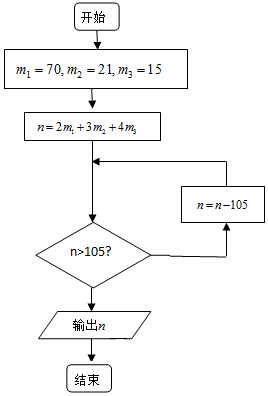 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子口诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此口诀的算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com