Question

设定义域为R的函数f（x）=

5|x-1|-1，x≥0 x2+4x+4，x＜0

，若关于x的方程f²（x）-（2m+1）f（x）+m²=0有5个不同的实数解，则m=

 

．

Answer 1

考点：根的存在性及根的个数判断,分段函数的应用

专题：计算题,函数的性质及应用

分析：故先根据题意作出f（x）的简图，令t=f（x），则由题意可得关于t的方程t²-（2m+1）t+m²=0有一根为t=4，另一个根大于4或等于0，把t=4代入方程t²-（2m+1）t+m²=0，求得m=2或m=6．经过检验，只有m=6满足条件．

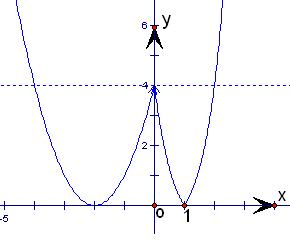
解答： 解：∵题中原方程f²（x）-（2m+1）f（x）+m²=0有5个不同的实数根，结合函数f（x）的图象可得，
令t=f（x），则关于t的方程t²-（2m+1）t+m²=0有一根为t=4，另一个根大于4或等于0．
把t=4代入方程t²-（2m+1）t+m²=0求得m=2或m=6．
当m=2时，关于t的方程t²-（2m+1）t+m²=0有一根为t=4，另一个根等于1，不满足条件．
当m=6时，关于t的方程t²-（2m+1）t+m²=0有一根为t=4，另一个根等于9，满足条件．
故答案为：6．

点评：本题主要考查方程的根的存在性以及根的个数判断，数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷，属于中档题．