
分析 (1)将a的值带入f(x),通过讨论x的范围,求出不等式的解集即可;
(2)求出f(x)的最小值,根据绝对值不等式成立条件得到当且仅当(2x-1)(x-a)≤0,通过讨论a的范围求出x的范围即可.
解答 解:(1)当a=-1时,
$f(x)=|{2x-1}|+|{x+1}|=\left\{\begin{array}{l}-3x(x≤-1)\\-x+2(-1<x<\frac{1}{2})\\ 3x(x≥\frac{1}{2})\end{array}\right.$,
当x≤-1时,-3x≥4,此时$x≤-\frac{4}{3}$,
当$-1<x<\frac{1}{2}$时,-x+2≥4,x无解
当$x≥\frac{1}{2}$时,3x≥4,此时$x≥\frac{4}{3}$,综上:$x≤-\frac{4}{3}$或$x≥\frac{4}{3}$
不等式解集为$\left\{{x\left|{\;}\right.x≤-\frac{4}{3}或x≥\frac{4}{3}}\right\}$
(2)因为|2x-1|+|x-a|≥|(2x-1)-(x-a)|=|x-1+a|
由绝对值不等式成立条件可知:
当且仅当(2x-1)(x-a)≤0时成立
当$a>\frac{1}{2}$时,$\frac{1}{2}≤x≤a$
当$a=\frac{1}{2}$时,$x=\frac{1}{2}$
当$a<\frac{1}{2}$时,$a≤x≤\frac{1}{2}$.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | (1,4) | B. | [1,4) | C. | (2,4) | D. | [2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
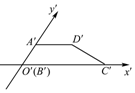 已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )
已知梯形ABCD是直角梯形,按照斜二测画法画出它的直观图A′B′C′D′(如图所示),其中A′D′=2,B′C′=4,A′B′=1,则直角梯形DC边的长度是( )| A. | $\sqrt{5}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某市为了增强市民的消防意识,面向社会招募社区宣传志愿者.现从20岁至45岁的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.若用分层抽样的方法从这100名志愿者中抽取20名参加消防演习活动,则从第4组中抽取的人数为4.
某市为了增强市民的消防意识,面向社会招募社区宣传志愿者.现从20岁至45岁的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.若用分层抽样的方法从这100名志愿者中抽取20名参加消防演习活动,则从第4组中抽取的人数为4.查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:选择题
有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为 ( )
A.2,4,6, 8 B.2,6,10,14
C.5,8,11,14 D.5,10,15,20
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一理下学期期末考数学试卷(解析版) 题型:选择题
四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程,分别得到以下四个结论:①y与x负相关且 =2.347x-6.423;②y与x负相关且
=2.347x-6.423;②y与x负相关且 =-3.476x+5.648;③y与x正相关且
=-3.476x+5.648;③y与x正相关且 =5.437x+8.493;④y与x正相关且
=5.437x+8.493;④y与x正相关且 =-4.326x-4.578.其中一定不正确的结论的序号是( )
=-4.326x-4.578.其中一定不正确的结论的序号是( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com