
| A�� | ǡ��һ����С����Ϊ1�����ڵ㣬ǡ��һ����С����Ϊ2�����ڵ� | |
| B�� | ǡ��һ����С����Ϊ1�����ڵ㣬ǡ��������С����Ϊ2�����ڵ� | |
| C�� | ǡ��������С����Ϊ1�����ڵ㣬ǡ��������С����Ϊ2�����ڵ� | |
| D�� | ǡ��������С����Ϊ1�����ڵ㣬ǡ���ĸ���С����Ϊ2�����ڵ� |
���� ���÷ֶκ�����ʾf��x��������f��x��=x���ⷽ�̿ɵú���f��x��ǡ��������С����Ϊ1�����ڵ㣻�ٽ�f��f��x����д�ɷֶκ�������f��f��x����=x���ⷽ�̿ɵú���f��x��ǡ���ĸ���С����Ϊ2�����ڵ㣮���ɵõ����ۣ�
��� �⣺f��x��=1-|2x-1|=$\left\{\begin{array}{l}{2-2x��x��\frac{1}{2}}\\{2x��x��\frac{1}{2}}\end{array}\right.$��
��f��x��=x����2-2x=x�����x=$\frac{2}{3}$��
��2x=x�����x=0��
������f��x��ǡ��������С����Ϊ1�����ڵ㣻
f��f��x����=1-|2��1-|2x-1|��-1|=$\left\{\begin{array}{l}{4x��x��\frac{1}{4}}\\{2-4x��\frac{1}{4}��x��\frac{1}{2}}\\{4x-2��\frac{1}{2}��x��\frac{3}{4}}\\{4-4x��x��\frac{3}{4}}\end{array}\right.$��
��f��f��x����=x��
��4x=x���ɵ�x=0����2-4x=x�����x=$\frac{2}{5}$��
��4x-2=x�����x=$\frac{2}{3}$����4-4x=x�����x=$\frac{4}{5}$��
���к���f��x��ǡ���ĸ���С����Ϊ2�����ڵ㣮
��ѡD��
���� ���⿼�麯�������ʺ����ã���Ҫ�����¶������������ã�����ֶκ��������ã�ע��ȥ����ֵ�ķ������������������������е��⣮


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{31}{16}$ | B�� | $\frac{31}{32}$ | C�� | 31 | D�� | 15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
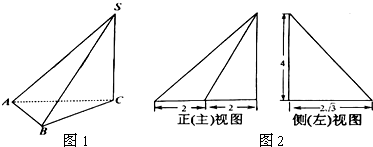
 һ�������������ͼ��ͼ������ͼ�Ͳ���ͼ������һ����Բ��һ���߳�Ϊ2����������ɣ�����ͼ��һ��Բ�������������ı����Ϊ7�У�
һ�������������ͼ��ͼ������ͼ�Ͳ���ͼ������һ����Բ��һ���߳�Ϊ2����������ɣ�����ͼ��һ��Բ�������������ı����Ϊ7�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com