
分析 设每天派出A型车x辆,B型车y辆,由题意列出约束条件,作出可行域,求出使目标函数取得最小值的整解得答案.
解答 解:设每天派出A型车x辆,B型车y辆,则A型车每天运物96x(0≤x≤8)吨,每天往返成本费240x元;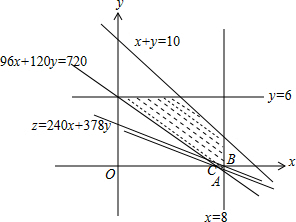
B型车每天运物120y(0≤y≤4)吨,每天往返成本费378y元;
公司总成本为z=240x+378y,
满足约束条件的可行域$\left\{\begin{array}{l}{0≤x≤8}\\{0≤y≤6}\\{x+y≤10}\\{96x+120y≥720}\end{array}\right.$如图示:
由图可知,当x=8,y=-0.4时,z有最小值,但是A(0,-0.4)不合题意,
目标函数向上平移过C(7.5,0)时,不是整解,继续上移至B(8,0)时,
z=240×8+378×0=1920有最小值,最小值为1920元.
即当每天应派出A型车8辆、B型车0辆,能使公司总成本最低,最低成本为1920元.
点评 本题解题的关键是列出不等式组(方程组)寻求约束条件,并就题目所述找出目标函数,同时注意整点的选取,是中档题.


科目:高中数学 来源: 题型:解答题
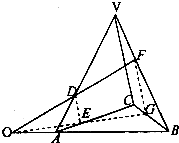 在三棱锥V-ABC中,D、E、F分别是VA、VB、VC上的点并且$\frac{AD}{AV}$=$\frac{AE}{AC}$=$\frac{VF}{VB}$=$\frac{CG}{CB}$=$\frac{1}{3}$.求证:直线DF、EG、AB共点.
在三棱锥V-ABC中,D、E、F分别是VA、VB、VC上的点并且$\frac{AD}{AV}$=$\frac{AE}{AC}$=$\frac{VF}{VB}$=$\frac{CG}{CB}$=$\frac{1}{3}$.求证:直线DF、EG、AB共点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正方体ABCD-A1B1C1D1中,E,F分别为BB1,DD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E,F分别为BB1,DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤-2或x≥$\frac{1}{2}$} | B. | {x|x≤-$\frac{1}{2}$或x≥2} | C. | {x|-$\frac{1}{2}$≤x≤2} | D. | {x|-2≤x≤$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com