
已知椭圆具有性质:若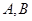 是椭圆
是椭圆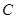 :
: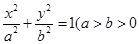 且
且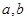 为常数
为常数 上关于原点对称的两点,点
上关于原点对称的两点,点 是椭圆上的任意一点,若直线
是椭圆上的任意一点,若直线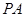 和
和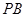 的斜率都存在,并分别记为
的斜率都存在,并分别记为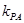 ,
,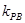 ,那么
,那么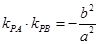 .类比双曲线
.类比双曲线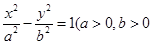 且
且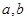 为常数
为常数 中,若
中,若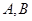 是双曲线
是双曲线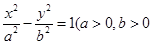 且
且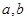 为常数
为常数 上关于原点对称的两点,点
上关于原点对称的两点,点 是双曲线上的任意一点,若直线
是双曲线上的任意一点,若直线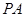 和
和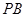 的斜率都存在,并分别记为
的斜率都存在,并分别记为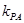 ,
,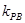 ,那么 .
,那么 .
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:单选题
在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
| A.1:2 | B.1:4 | C.1:6 | D.1:8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
请阅读下列材料:若两个正实数a1,a2满足a12+a22=1,那么a1+a2≤ .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以Δ≤0,从而得4(a1+a2)2-8≤0,所以a1+a2≤ .
.
根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com