
分析 由题意可得$\frac{1}{x}+\frac{1}{y}$=($\frac{1}{x}+\frac{1}{y}$)(2x+y)=3+$\frac{y}{x}$+$\frac{2x}{y}$,由基本不等式可得.
解答 解:∵2x+y=1,且x>0,y>0,
∴$\frac{1}{x}+\frac{1}{y}$=($\frac{1}{x}+\frac{1}{y}$)(2x+y)
=3+$\frac{y}{x}$+$\frac{2x}{y}$≥3+2$\sqrt{\frac{y}{x}•\frac{2x}{y}}$=3+2$\sqrt{2}$
当且仅当$\frac{y}{x}$=$\frac{2x}{y}$时取等号,
结合2x+y=1可得x=$\frac{2-\sqrt{2}}{2}$且y=$\sqrt{2}$-1,
故答案为:3+2$\sqrt{2}$
点评 本题考查基本不等式求最值,“1”的代换是解决问题的关键,属基础题.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a+b)2≥16 | B. | (a+b)2≤16 | C. | (a-b)2≥16 | D. | (a-b)2≤16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
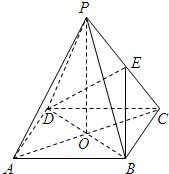 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k<-$\frac{1}{2}$ | B. | k>-$\frac{1}{2}$ | C. | k<$\frac{1}{2}$ | D. | k>$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-1与y=$\sqrt{(x-1)^{2}}$ | B. | y=$\sqrt{x-1}$与y=$\frac{x-1}{\sqrt{x-1}}$ | ||
| C. | y=$\sqrt{x-1}$•$\sqrt{x+1}$与y=$\sqrt{(x+1)(x-1)}$ | D. | y=$\frac{x}{x}$与y=x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x(x≥0)}\\{-x(x<0)}\end{array}\right.$ | B. | f(x)=$\frac{{x}^{2}-4}{x-2}$,g(x)=x+2 | ||
| C. | f(x)=$\sqrt{{x}^{2}}$,g(x)=x+2 | D. | f(x)=$\sqrt{1-{x}^{2}}$+$\sqrt{{x}^{2}-1}$,g(x)=0,x∈{-1,1}. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com