
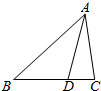
 如图所示,在△ABC中,D为BC边上的一点,且BD=2DC,若$\overrightarrow{AC}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n∈R),则$\frac{n}{m}$=-3.
如图所示,在△ABC中,D为BC边上的一点,且BD=2DC,若$\overrightarrow{AC}$=m$\overrightarrow{AB}$+n$\overrightarrow{AD}$(m,n∈R),则$\frac{n}{m}$=-3. 分析 根据向量减法的几何意义,以及向量的数乘运算便可由$\overrightarrow{BD}=2\overrightarrow{DC}$得到$\overrightarrow{AC}=-\frac{1}{2}\overrightarrow{AB}+\frac{3}{2}\overrightarrow{AD}$,这便可得到m=$-\frac{1}{2},n=\frac{3}{2}$,从而可以求出$\frac{n}{m}$.
解答 解:BD=2DC;
∴$\overrightarrow{BD}=2\overrightarrow{DC}$;
∴$\overrightarrow{AD}-\overrightarrow{AB}=2(\overrightarrow{AC}-\overrightarrow{AD})$;
∴$\overrightarrow{AC}=-\frac{1}{2}\overrightarrow{AB}+\frac{3}{2}\overrightarrow{AD}$;
又$\overrightarrow{AC}=m\overrightarrow{AB}+n\overrightarrow{AD}$;
∴$m=-\frac{1}{2},n=\frac{3}{2}$;
∴$\frac{n}{m}=-3$.
故答案为:-3.
点评 考查向量数乘、减法的几何意义,以及向量的数乘运算,平面向量基本定理.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
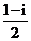 .
.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
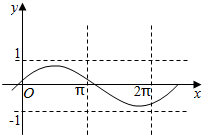
| A. | f(x)=$\frac{3}{4}$sin($\frac{3}{2}$x+$\frac{π}{6}$) | B. | f(x)=$\frac{4}{5}$sin($\frac{4}{5}$x+$\frac{1}{5}$) | C. | f(x)=$\frac{4}{5}$sin($\frac{5}{6}$x+$\frac{π}{6}$) | D. | f(x)=$\frac{4}{5}$sin($\frac{2}{3}$x-$\frac{1}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com