练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知等边△ABC中，点P在线段AB上，且
    AP
    =λ
    PB
    ，若
    CP
    •
    AB
    =
    PA
    •
    PB
    ，则实数λ的值为（　　）
    A、2
    B、
    		2
    2
    C、
    		2
    -1
    D、
    		2
    +1
    考点：平面向量数量积的运算
    专题：平面向量及应用
    分析：将
    CP
    •
    AB
    =
    PA
    •
    PB
    利用已知三角形的三边对于向量表示，然后得到关于λ的等式解之．
    解答： 解：因为等边△ABC中，点P在线段AB上，且
    AP
    =λ
    PB
    ，
    由
    CP
    •
    AB
    =
    PA
    •
    PB
    ，
    得（
    CA
    +
    AP
    ）
    AB
    =-λ
    PB
    2    ，
    所以-
    1
    2
    AB
    2    +
    λ
    1+λ
    AB
    2    =-λ×
    1
    (1+λ)2
    AB
    2    ，
    所以-
    1
    2
    +
    λ
    1+λ
    =
    -λ
    (1+λ)2
    ，解得λ=±
    		2
    -1    ，由点P在线段AB上，且
    AP
    =λ
    PB
    ，得λ＞0，
    所以λ=
    		2
    -1    ；
    故选C．
    点评：本题考查了向量的数量积运算，考查学生的运算能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某公司准备将1000万元资金投入到市环保工程建设中，现有甲、乙两个建设项目选择，若投资甲项目一年后可获得的利润ξ1（万元）的概率P分布列如表所示：
    ξ1  110 120170 
    P m  0.4n 
    且ξ1的期望E（ξ1）=120；若投资乙项目一年后可获得的利润ξ2（万元）与该项目建设材料的成本有关，在生产的过程中，公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整，两次调整相互独立且调整的概率分别为p（0＜p＜1）和1-p，乙项目产品价格一年内调整次数X（次）与ξ2的关系如表所示：
    X（次）  01 2 
     ξ2 41.2 117.6204.0 
    （1）求m，n的值；
    （2）求ξ1的分布列；
    （3）若E（ξ1）＜E（ξ2）则选择投资乙项目，求此时P的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=2cosx（sinx+
    		3
    cosx）．
    （1）求函数f（x）的值域最小正周期；
    （2）若随任意函数x∈[0，
    π
    6
    ]，则|f（x）-
    		3
    |+2＞m恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    甲乙两名射击手的测试成绩统计如下：
    第一次第二次第三次第四次第五次
    甲命中环数688810
    乙命中环数1061068
    甲乙两名射击手都很优秀，现只能挑选一名射击手参加比赛，若你是教练，你认为挑选哪一位比较适宜？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

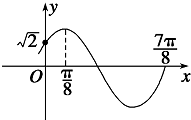    函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
    π
    2
    ）的一段图象（如图所示） 
    （1）求其解析式；
    （2）令g（x）=
    f2(x)-2f(x)+2
    f(x)-1
    ，当x∈[0，
    π
    4
    ]时，求g（x）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某校有五年级学生120人，现要从中随机抽取10人参加校义务活动，现将学生统一随机编号为1，2，3…120号，下列哪种是系统抽样抽取的号码（　　）
    A、2，10，22，34，56，68，80，92，104，116
    B、5，15，25，35，55，65，75，85，95，115
    C、6，18，30，42，54，66，78，90，102，114
    D、14，26，38，50，62，70，82，94，106，118

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若两平行直线3x-2y-1=0和3x-2y+c=0之间的距离为
    2
    		13
    13
    ，则c=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）=ax-（k-1）a-x（a＞0且a≠1）是定义域为R的奇函数．
    （Ⅰ）求k值；
    （Ⅱ）若f（1）＜0，求使不等式f（x2+tx）+f（4-x）＜0恒成立的实数t的取值范围；
    （Ⅲ）若f（1）=
    3
    2
    ，且g（x）=a2x+a-2x-2mf（x）在[1，+∞）上的最小值为-2，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f（x）定义在区间（0，+∞）上的减函数，且满足f（x•y）=f（x）+f（y），并且f(
    1
    3
    )=1
    （1）求f（1）
    （2）求f(
    1
    9
    )
    （3）若f（x）+f（1-2x）＜2，求x的范围．

    查看答案和解析>>

    同步练习册答案