
分析 将原不等式化为(ax+2)(x-1)<0分a=0,a>0,a<0三种情况进行讨论.a=0、a>0易解不等式;当a<0时,按照对应方程的两根大小分三种情况讨论即可.
解答 解:将原不等式化为(ax+2)(x-1)<0,
(1)当a=0时,有x<1;
(2)当a>0时,有(x+$\frac{2}{a}$)(x-1)<0,解得-$\frac{2}{a}$<x<1,
(3)当a<0时,有(x+$\frac{2}{a}$)(x-1)>0,
若-$\frac{2}{a}$>1时,即-2<a<0,解得x<1或x>-$\frac{2}{a}$,
若-$\frac{2}{a}$=1时,即a=-2,解得x≠1,
若-$\frac{2}{a}$<1时,即a<-2,解得x<-$\frac{2}{a}$,或x>1,
综上,a=0时,不等式的解集为{x|x<1};-2<a<0时,不等式的解集为{x|x<1或x>-$\frac{2}{a}$};
当a=-2时,不等式的解集为{x|x∈R,且x≠1};
当a<-2时,不等式的解集为{x|x<-$\frac{2}{a}$或x>1};
当a>0时,不等式的解集为{x|-$\frac{2}{a}$<x<1}.
点评 本题考查了含有字母系数的一元二次不等式的解法问题,解题时需要分类讨论,是易错题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
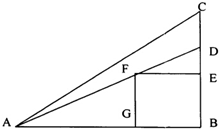 如图,某小区准备在一直角围墙ABC内的空地上植造“绿地△ABD”,其中AB=a,BD长可根据需要进行调节(BC足够长),现规划在△ABD内接正方形BEFG内种花,其余地方种草,设种草的面积S1与种花的面积S2的比$\frac{S_1}{S_2}$为y.
如图,某小区准备在一直角围墙ABC内的空地上植造“绿地△ABD”,其中AB=a,BD长可根据需要进行调节(BC足够长),现规划在△ABD内接正方形BEFG内种花,其余地方种草,设种草的面积S1与种花的面积S2的比$\frac{S_1}{S_2}$为y.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com