
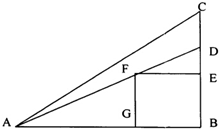
 如图,某小区准备在一直角围墙ABC内的空地上植造“绿地△ABD”,其中AB=a,BD长可根据需要进行调节(BC足够长),现规划在△ABD内接正方形BEFG内种花,其余地方种草,设种草的面积S1与种花的面积S2的比$\frac{S_1}{S_2}$为y.
如图,某小区准备在一直角围墙ABC内的空地上植造“绿地△ABD”,其中AB=a,BD长可根据需要进行调节(BC足够长),现规划在△ABD内接正方形BEFG内种花,其余地方种草,设种草的面积S1与种花的面积S2的比$\frac{S_1}{S_2}$为y.分析 (1)由于题目中“设∠DAB=θ,”,故可利用解三角形的知识解决“草花比y”;
(2)由于式子“y=$\frac{1}{2}$(tanθ+$\frac{1}{tanθ}$)≥1”括号中两式的积是定值,故利用二元不等式求其最小值.
解答 解:(1)因为BD=atanθ,
所△ABD的面积为$\frac{1}{2}$a2tanθ(θ∈(0,$\frac{π}{2}$)
设正方形BEFG的边长为t,则由$\frac{FG}{AB}=\frac{DG}{DB}$,
得$\frac{t}{a}$=$\frac{atanθ-t}{atanθ}$,
解得t=$\frac{atanθ}{1+tanθ}$,则S2=$\frac{{a}^{2}ta{n}^{2}θ}{(1+tanθ)^{2}}$
所以S1=$\frac{1}{2}$a2tanθ-S2,
所以$y=\frac{tanθ}{2}+\frac{1}{2tanθ}+1$,$θ∈(0,\frac{π}{2})$;
(2)因为tanθ∈(0,+∞),所以y=$\frac{1}{2}$(tanθ+$\frac{1}{tanθ}$)≥1
当且仅当tanθ=1,时取等号,此时BE=$\frac{a}{2}$.
所以$BE=\frac{a}{2}$,y最小值为2.
点评 本题主要考查函数在实际生活中的应用、解三角形以及利用基本不等式求函数最值的方法,解决实际问题通常有几个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果,其中关键是建立数学模型.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{18}^{11}$ | B. | C${\;}_{18}^{11}$ | C. | A${\;}_{18}^{10}$ | D. | C${\;}_{18}^{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com