练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．tan20°+tan40°+$\sqrt{3}$tan20°tan40°的值是（　　）
    A．60°B．$\sqrt{3}$C．1D．$\frac{\sqrt{3}}{3}$

    分析 由tan60°=tan（20°+40°），展开两角和的正切得答案．

    解答 解：∵$\sqrt{3}$=tan60°=tan（20°+40°）=$\frac{tan20°+tan40°}{1-tan20°tan40°}$，
    ∴$\sqrt{3}-\sqrt{3}tan20°tan40°=tan20°+tan40°$，
    则tan20°+tan40°+$\sqrt{3}$tan20°tan40°=$\sqrt{3}$．
    故选：B．

    点评 本题考查两角和的正切，是基础的计算题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=$\frac{f'（1）}{e}•{e^x}-f（0）•x+\frac{1}{2}{x^2}（e$是自然对数的底数）．
    （Ⅰ）求函数f（x）的解析式
    （Ⅱ）求函数f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．在Rt△ABC中，已知a＜b＜c，且a、b、c成等比数列，则a：c等于（　　）
    A．3：4B．（$\sqrt{5}$-1）：2C．1：（$\sqrt{5}$-1）D．$\sqrt{2}$：1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

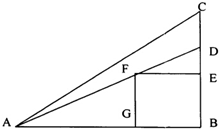    8．如图，某小区准备在一直角围墙ABC内的空地上植造“绿地△ABD”，其中AB=a，BD长可根据需要进行调节（BC足够长），现规划在△ABD内接正方形BEFG内种花，其余地方种草，设种草的面积S1与种花的面积S2的比$\frac{S_1}{S_2}$为y．
    （1）设角∠DAB=θ，将y表示成θ的函数关系；
    （2）当BE为多长时，y有最小值，最小值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如表数据：
    单价x（元）88.28.48.68.89
    销量y（件）908483807568
    （1）求销量y对单价x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
    （2）预计在今后的销售中，销量与单价仍服从（1）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价大概定为多少元？
    附：$\sum_{i=1}^6{x_i}$=51$\sum_{i=1}^6{y_i}$=480$\sum_{i=1}^6{x_i}{y_i}$=4066$\sum_{i=1}^6{x_i^2}$=434.2，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，其中$\overline{x}$，$\overline{y}$是样本平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．计算下列各式的值
    （1）已知sinα是方程5x2-7x-6=0的根，α是第三象限角，则计算$\frac{{sin（-α-\frac{3}{2}π）cos（\frac{3}{2}π-α）}}{{cos（\frac{π}{2}-α）sin（\frac{π}{2}+α）}}$•tan2（π-α）；
    （2）$\frac{\sqrt{1-2sin40°cos40°}}{cos40°-\sqrt{1-si{n}^{2}50°}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．（1）计算$\int_1^2$（$\frac{1}{{\sqrt{x}}}$+$\frac{1}{x^2}$）dx；
    （2）求由曲线y=$\sqrt{x}$，y=2-x，y=-$\frac{1}{3}$x所围成图形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．函数y=|sinx|的图象（　　）
    A．只关于x轴对称B．只关于y轴对称C．关于原点对称D．关于坐标轴对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．集合A={x|x2-x-2≤0}，B={x|x＜1，x∈Z}，则A∩B=（　　）
    A．[-1，1）B．[-1，2]C．{-1，0}D．{0，1}

    查看答案和解析>>

    同步练习册答案