
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
分析 (1)计算平均数,利用$\stackrel{∧}{b}$=-20,求出$\stackrel{∧}{a}$,即可求得回归直线方程;
(2)设工厂获得的利润为L元,利用利润=销售收入-成本,建立函数,利用配方法可求工厂获得的利润最大.
解答 解:(1)由已知可得:
$\overline{x}=\frac{1}{6}\sum_{i=1}^6{x_i}=\frac{51}{6}=8.5$,
$\sum_{i=1}^6{{x_i}^2}=434.2$,
$\overline{y}=\frac{1}{6}\sum_{i=1}^6{y_i}=\frac{480}{6}=80$,
$\sum_{i=1}^{6}{x}_{i}{y}_{i}$=4066.
∴$\hat b=\frac{4066-6×8.5}{434.2-6×8.5×8.5}=-\frac{14}{0.7}=-20$
∴$\hat a=80+8.5×20=250$
∴$\hat y=-20x+250$
(2)设工厂获得利润为L
则L=(x-4)(-20x+250)=-20x2+330x-1000,
当$x=\frac{330}{40}=8.25$时,y有最大值,
∴该产品的单价大概定为8.25元.
点评 本题考查线性回归方程,考查最小二乘法的应用,考查利用线性回归方程预报变量的值,是一个新课标中出现的新知识点,本题解题的关键是正确运算出线性回归方程系数的值,本题是一个中档题目.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
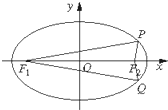 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,点P(3,1)在椭圆上,△PF1F2的面积为2$\sqrt{2}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,点P(3,1)在椭圆上,△PF1F2的面积为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}2x-1,x≥\frac{1}{2}\\ 1-2x,x<\frac{1}{2}\end{array}$.
已知函数f(x)=$\left\{\begin{array}{l}2x-1,x≥\frac{1}{2}\\ 1-2x,x<\frac{1}{2}\end{array}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com