
分析 (Ⅰ)由等比数列的性质,a4=a1•q3,即可求得q的值,即可求得数列数列{an}的通项公式,求得a3,根据等差数列性质,求得公差d,即可求得{bn}的通项公式;
(Ⅱ)由(Ⅰ)即可求得数列{cn}的通项公式,根据等比数列和等差数列前n项和公式,即可求得数列{cn}的前n项和.
解答 解:(Ⅰ)设等比数列{an}的公比为q,由题意,得${q^3}=\frac{a_4}{a_1}=\frac{24}{3}=8$,…(2分)
解得:q=2.…(3分)
∴${a_n}={a_1}{q^{n-1}}=3×{2^{n-1}}(n=1,2,…)$.…(4分)
∴a3=12.…(5分)
设等差数列{an}的公差为d,
∵b2=4,b4=12,
∵b4=b2+2d,
∴12=4+2d,
解得:d=4,
∴bn=b2+(n-2)d=4+(n-2)×4=4n-4,
bn=4n-4.…(8分)
(Ⅱ)由(Ⅰ)知${a_n}=3×{2^{n-1}}$,bn=4n-4,
因此${c_n}={a_n}-{b_n}=3×{2^{n-1}}-(4n-4)$.
从而数列{cn}的前n项和${S_n}=3+6+…+3×{2^{n-1}}-[0+4+8+…+(4n-4)]$…(9分)
=$3×\frac{{1-{2^n}}}{1-2}-\frac{n(4n-4)}{2}$…(11分)
=3×2n-3-n(2n-2)…(12分)
=3×2n-3-2n2+2n.…(13分)
点评 本题考查等差数列和等比数列通项公式,考查数列前n项和公式,考查计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
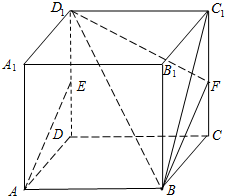 在正方体ABCD-A1B1C1D1中,E、F分别为DD1、CC1的中点.
在正方体ABCD-A1B1C1D1中,E、F分别为DD1、CC1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com