
分析 (1)利用倍角公式与辅助角公式将f(x)=sin($\frac{π}{4}$+x)sin($\frac{π}{4}$-x)+$\sqrt{3}$sinxcosx化为:f(x)=sin(2x+$\frac{π}{6}$),即可求得f($\frac{π}{6}$)的值;
(2)由A为三角形的内角,f(A)=sin(2A+$\frac{π}{6}$)=1可求得A=$\frac{π}{6}$,从而sinB+sinC=sinB+sin($\frac{5π}{6}$-B),展开后利用三角函数的辅助角公式即可求得sinB+sinC的最大值.
解答 (1)∵f(x)=sin($\frac{π}{4}$+x)sin($\frac{π}{4}$-x)+$\sqrt{3}$sinxcosx=$\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x,
sin(2x+$\frac{π}{6}$),
∴f($\frac{π}{6}$)=1;
(2)f(A)=sin(2A+$\frac{π}{6}$)=1,
而0<A<π可得:2A+$\frac{π}{6}$=$\frac{π}{2}$,即A=$\frac{π}{6}$.
∴sinB+sinC=sinB+sin($\frac{5π}{6}$-B)=$\frac{3}{2}$sinB+$\frac{\sqrt{3}}{2}$cosB=$\sqrt{3}$sin(B+$\frac{π}{3}$).
∵0<B<$\frac{2π}{3}$,
∴$\frac{π}{3}$<B+$\frac{π}{3}$<π,0<sin(B+$\frac{π}{3}$)≤1,
∴sinB+sinC的最大值为$\sqrt{3}$.
点评 本题考查三角函数的恒等变换及化简求值,着重考查三角函数的辅助角公式的应用,考查分析与推理能力,属于中档题.


科目:高中数学 来源:2017届湖北省百所重点校高三联合考试数学(文)试卷(解析版) 题型:解答题
已知函数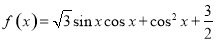 .
.
(1)当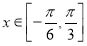 时,求函数
时,求函数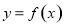 的值域;
的值域;
(2)已知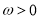 ,函数
,函数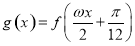 ,若函数
,若函数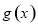 在区间
在区间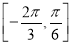 上是增函数,求
上是增函数,求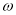 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(文)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数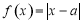 ,
,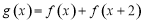 .
.
(Ⅰ)当 时,解不等式:
时,解不等式: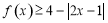 ;
;
(Ⅱ)若关于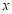 的不等式
的不等式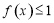 的解集为
的解集为 ,求证:
,求证: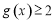 .
.
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数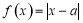 ,
,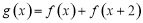 .
.
(Ⅰ)当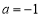 时,解不等式:
时,解不等式: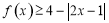 ;
;
(Ⅱ)若关于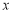 的不等式
的不等式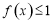 的解集为
的解集为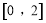 ,求证:
,求证: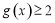 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com