
已知函数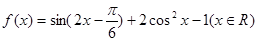
(1)求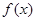 的单调递增区间;
的单调递增区间;
(2)在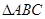 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为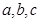 ,已知
,已知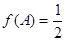 ,
,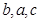 成等差数列,且
成等差数列,且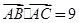 ,求边
,求边 的值.
的值.
(1)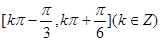 ;(2)
;(2)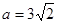 .
.
解析试题分析:(1)求三角函数的单调区间等问题,我们的目标很明确,就是要把函数化为 的形式,然后根据正弦函数的性质得出结论,本题中首先把
的形式,然后根据正弦函数的性质得出结论,本题中首先把
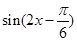 用两角差的正弦公式展开,再把
用两角差的正弦公式展开,再把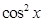 降幂把角化为
降幂把角化为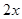 ,即化为同角的问题,再利用两角和或差的正弦公式,转化为一个三角函数;(2)已知
,即化为同角的问题,再利用两角和或差的正弦公式,转化为一个三角函数;(2)已知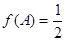 ,由(1)的结论应该很容易求出角A,
,由(1)的结论应该很容易求出角A,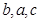 成等差数列得一个关系
成等差数列得一个关系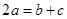 ,
,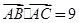 可以转化为
可以转化为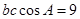 ,从而
,从而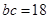 ,这是第二个关系,但其中有三个未知数
,这是第二个关系,但其中有三个未知数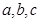 ,还需找一个关系式,
,还需找一个关系式,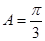 ,这里我们联想到余弦定理,正好找到第三个关系,从而联立方程组求出边
,这里我们联想到余弦定理,正好找到第三个关系,从而联立方程组求出边 .
.
试题解析:解:(1)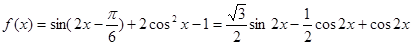
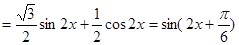
令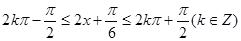
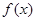 的单调递增区间为
的单调递增区间为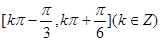
(2)由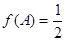 ,得
,得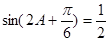
∵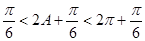 ,∴
,∴ ,∴
,∴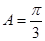
由b,a,c成等差数列得2a=b+c
∵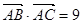 ,∴
,∴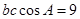 ,∴
,∴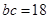
由余弦定理,得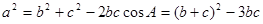
∴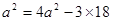 ,∴
,∴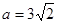
考点:(1)三角函数的单调性;(2)等差数列,向量的数量积定义,余弦定理.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
设函数 ,其中角
,其中角 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与 轴非负半轴重合,
轴非负半轴重合,
终边经过点 ,且
,且 .
.
(1)若点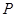 的坐标为
的坐标为 ,求
,求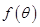 的值;
的值;
(2)若点 为平面区域
为平面区域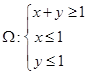 上的一个动点,试确定角
上的一个动点,试确定角 的取值范围,并求函数
的取值范围,并求函数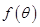 的最小值和最大值.
的最小值和最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com