
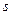 km,汽车从甲地匀速行驶到乙地,速度不得超过
km,汽车从甲地匀速行驶到乙地,速度不得超过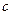 km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度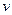 km/h的平方成正比,比例系数为
km/h的平方成正比,比例系数为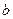 ,固定部分为
,固定部分为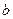 元.
元.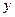 (元)表示为
(元)表示为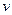 速度(千米/时)的函数,并指出这个函数的定义域;
速度(千米/时)的函数,并指出这个函数的定义域;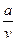 +bv),v∈
+bv),v∈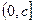 .
.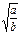 ≤c时,行驶速度为v=
≤c时,行驶速度为v=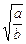 ;当
;当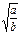 >c时,行驶速度为v=c.
>c时,行驶速度为v=c.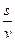 ,全程运输成本为y=a·
,全程运输成本为y=a·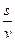 +bv2·
+bv2·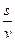 =s(
=s(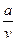 +bv).
+bv).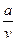 +bv),v∈
+bv),v∈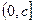 .
.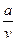 +bv)≥2s
+bv)≥2s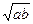 .当且仅当
.当且仅当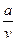 =bv,即v=
=bv,即v=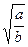 时上式中等号成立.
时上式中等号成立.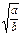 ≤c时,则当v=
≤c时,则当v=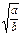 时全程运输成本最小;
时全程运输成本最小;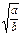 >c时,则当v∈
>c时,则当v∈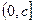 时有s(
时有s(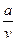 +bv)-s(
+bv)-s(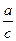 +bc)=s[(
+bc)=s[(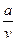 -
-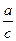 )+(bv-bc)]=
)+(bv-bc)]=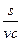 (c-v)(a-bcv).
(c-v)(a-bcv).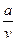 +bv)≥s(
+bv)≥s(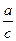 +bc),当且仅当v=c时等号成立.
+bc),当且仅当v=c时等号成立.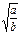 ≤c时,行驶速度为v=
≤c时,行驶速度为v=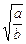 ;当
;当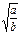 >c时,行驶速度为v=c.
>c时,行驶速度为v=c.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源:不详 题型:解答题
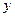 万元与投入
万元与投入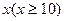 万元之间满足:
万元之间满足: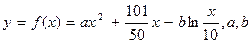 为常数。当
为常数。当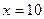 万元时,
万元时,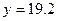 万元;当
万元;当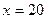 万元时,
万元时,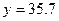 万元。(参考数据:
万元。(参考数据: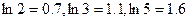 )
)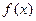 的解析式;
的解析式;
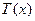 的最大值。(利润=旅游增加值-投入)
的最大值。(利润=旅游增加值-投入)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
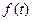 与时间
与时间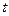 满足关系
满足关系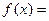 {
{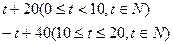 ,销售量
,销售量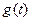 与时间
与时间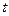 满足关系
满足关系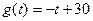 ,
,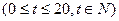 ,设商品的日销售额为
,设商品的日销售额为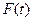 (销售量与价格之积).
(销售量与价格之积).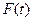 的解析式;
的解析式;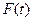 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
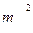 的厂房(不管墙高),工程的造价是:
的厂房(不管墙高),工程的造价是:查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
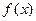 是定义在R上的偶函数,且对于任意的
是定义在R上的偶函数,且对于任意的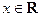 恒有
恒有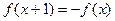 ,已知当
,已知当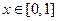 时,
时,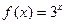 .则
.则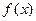 的周期;
的周期;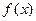 在(2,3)上是增函数;
在(2,3)上是增函数;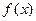 的最大值为1,最小值为0;
的最大值为1,最小值为0;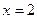 是函数
是函数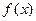 图象的一条对称轴.
图象的一条对称轴.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 +r=0的解集分别为A、B且A≠B,A∪B={-3,4 },A∩B={-3},求p,q,r的值.
+r=0的解集分别为A、B且A≠B,A∪B={-3,4 },A∩B={-3},求p,q,r的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com