
分析 (1)由代入和解方程,可得840+15k=1245的解;
(2)设楼房每平方米的平均综合费用为f(x)元,可得f(x)=(840+27x)+$\frac{3240×10000}{3000x}$,求出导数和单调区间,可得极小值点,且为最小值点.
解答 解:(1)由题意可得840+15k=1245,解得k=27;
(2)设楼房每平方米的平均综合费用为f(x)元,
则f(x)=(840+27x)+$\frac{3240×10000}{3000x}$=840+27x+$\frac{10800}{x}$,x>0且x∈N*,
f′(x)=27-$\frac{10800}{{x}^{2}}$,令f′(x)=0得x=20,
| x | (0,20) | x=20 | (20,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 递减 | 极小值 | 递增 |
点评 本题考查导数在实际问题中的应用:求最值,考查化简整理的运算能力,正确列出函数的解析式和求出导数是解题的关键,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
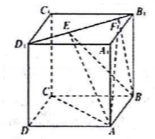 如图,正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F,且EF=$\sqrt{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F,且EF=$\sqrt{2}$,则下列结论中错误的是( )| A. | AC⊥BE | B. | EF∥平面ABCD | ||
| C. | 异面直线AE,BF所成的角为定值 | D. | 三棱锥B-AEF的体积为定值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,AB∥CD,PA=PD=AD=1,DC=2AB=4AD,∠ADC=120°,E为PC的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥底面ABCD,AB∥CD,PA=PD=AD=1,DC=2AB=4AD,∠ADC=120°,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com