
分析 分类讨论以去掉绝对值号,从而利用基本不等式确定各自方程的根的个数,从而解得.
解答 解:当x≥$\frac{2\sqrt{5}}{5}$时,5x-$\frac{4}{x}$≥0,
∵方程(4x+$\frac{5}{x}$)-|5x-$\frac{4}{x}$|=m,
∴(4x+$\frac{5}{x}$)-(5x-$\frac{4}{x}$)=m,即-x+$\frac{9}{x}$=m;
∴m≤$\frac{41}{10}\sqrt{5}$.
当0<x<$\frac{2\sqrt{5}}{5}$时,5x-$\frac{4}{x}$<0,
∵方程(4x+$\frac{5}{x}$)-|5x-$\frac{4}{x}$|=m,
∴(4x+$\frac{5}{x}$)+(5x-$\frac{4}{x}$)=m,
即9x+$\frac{1}{x}$=m;
∵9x+$\frac{1}{x}$≥6;
∴当m<6时,方程9x+$\frac{1}{x}$=m无解;
当m=6时,方程9x+$\frac{1}{x}$=m有且只有一个解;
当6<m<10时,方程9x+$\frac{1}{x}$=m在(0,1)上有两个解;
当m=10时,方程9x+$\frac{1}{x}$=m的解为1,$\frac{1}{9}$;
综上所述,实数m的取值范围为(6,$\frac{41}{10}\sqrt{5}$).
故答案为:(6,$\frac{41}{10}\sqrt{5}$).
点评 本题考查了绝对值方程的解法与应用,同时考查了基本不等式的应用及转化思想的应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
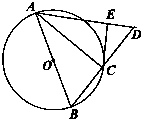 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC=( )
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC=( )| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
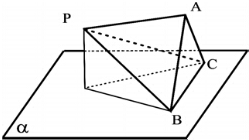 已知正三棱锥P-ABC底面边长为6,底边BC在平面α内,绕BC旋转该三棱锥,若某个时刻它在平面α上的正投影是等腰直角三角形,则此三棱锥高的取值范围是( )
已知正三棱锥P-ABC底面边长为6,底边BC在平面α内,绕BC旋转该三棱锥,若某个时刻它在平面α上的正投影是等腰直角三角形,则此三棱锥高的取值范围是( )| A. | (0,$\sqrt{6}$] | B. | (0,$\frac{\sqrt{6}}{2}$]∪[$\sqrt{6}$,3] | C. | (0,$\frac{\sqrt{6}}{2}$] | D. | (0,$\sqrt{6}$]∪[3,$\frac{3\sqrt{6}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com