
分析 (1)将直线l的参数方程中两式相减可得直线l的普通方程;由ρ2sin2θ=2ρcosθ,代入x=ρcosθ,y=ρsinθ,可得曲线C的直角坐标方程;
(2)联立直线l和曲线C的普通方程,解方程可得交点A,B,运用两点的距离公式和点到直线的距离公式,结合三角形的面积公式,计算即可得到所求值.
解答 解:(1)直线l的参数方程为$\left\{{\begin{array}{l}{x=1+t}\\{y=t-3}\end{array}}\right.$(t为参数),
两式相减可得x-y=4,即有直线l的普通方程为x-y-4=0:
曲线C的极坐标方程为$ρ=\frac{2cosθ}{{{{sin}^2}θ}}$,即ρ2sin2θ=2ρcosθ,
代入x=ρcosθ,y=ρsinθ,可得y2=2x;
(2)联立方程x-y-4=0和方程y2=2x,
消去y,可得x2-10x+16=0,
解得x1=2,x2=8,
可得交点A(2,-2),B(8,4),
即有|AB|=$\sqrt{(2-8)^{2}+(-2-4)^{2}}$=6$\sqrt{2}$,
O到直线l的距离为d=$\frac{|0-0-4|}{\sqrt{2}}$=2$\sqrt{2}$,
则△AOB的面积为S=$\frac{1}{2}$d•|AB|=$\frac{1}{2}$×2$\sqrt{2}$×6$\sqrt{2}$=12.
点评 本题考查极坐标方程、参数方程化为直角坐标方程,注意运用极坐标和直角坐标的互化公式和代入法,考查直线和抛物线方程联立,求交点,运用点到直线的距离公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于极轴所在直线对称 | B. | 关于极点对称 | ||
| C. | 重合 | D. | 关于直线θ=$\frac{π}{2}$(ρ∈R)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
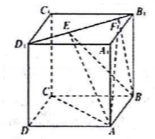 如图,正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F,且EF=$\sqrt{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F,且EF=$\sqrt{2}$,则下列结论中错误的是( )| A. | AC⊥BE | B. | EF∥平面ABCD | ||
| C. | 异面直线AE,BF所成的角为定值 | D. | 三棱锥B-AEF的体积为定值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com