
分析 化简方程求出m的表达式,然后利用方程是否有意义,分别求解m的范围,通过函数的最值(利用基本不等式),求解即可.
解答 解:方程lg$\frac{2}{x}$=lg(m-8x),
当x≤0时,此时lg$\frac{2}{x}$没有意义,方程解集为空集.
当x>0,可得:$\frac{2}{x}$=m-8x,即m=$\frac{2}{x}$+8x,
即m=$\frac{2}{x}$+8x≥2$\sqrt{\frac{2}{x}•8x}$=8,当且仅当x=$\frac{1}{2}$时取等号,
因为:方程lg$\frac{2}{x}$=lg(m-8x)的解集为∅,
所以m<8.
综上m<8.
故答案为:m<8
点评 本题考查函数与方程的综合应用,方程的解集基本不等式的应用,函数恒成立,考查分析问题解决问题的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
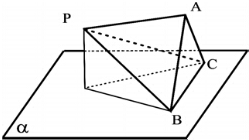 已知正三棱锥P-ABC底面边长为6,底边BC在平面α内,绕BC旋转该三棱锥,若某个时刻它在平面α上的正投影是等腰直角三角形,则此三棱锥高的取值范围是( )
已知正三棱锥P-ABC底面边长为6,底边BC在平面α内,绕BC旋转该三棱锥,若某个时刻它在平面α上的正投影是等腰直角三角形,则此三棱锥高的取值范围是( )| A. | (0,$\sqrt{6}$] | B. | (0,$\frac{\sqrt{6}}{2}$]∪[$\sqrt{6}$,3] | C. | (0,$\frac{\sqrt{6}}{2}$] | D. | (0,$\sqrt{6}$]∪[3,$\frac{3\sqrt{6}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
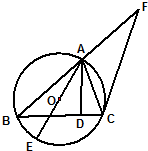 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆台是直角梯形绕其一边旋转而成的旋转体 | |
| B. | 棱台的上下底面一定相似,但侧棱长不一定相等 | |
| C. | 顶点在底面的投影为底面中心的棱锥为正三棱锥 | |
| D. | 圆锥是直角三角形绕其一边旋转而成的旋转体 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
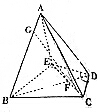 如图所示,在四棱锥A-BCDEE中,AE⊥面BCDE,△BCE是正三角形,BD和CE的交点F恰好平分CE.又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.
如图所示,在四棱锥A-BCDEE中,AE⊥面BCDE,△BCE是正三角形,BD和CE的交点F恰好平分CE.又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com