
分析 (Ⅰ)法1:求函数的导数f′(x),构造函数g(x)=(x-2)-(x-1)ln(x-1)(x>2),利用导数判断函数的单调性即可,
法2:求函数的导数构造函数$g(x)=\frac{x-2}{x-1}-ln(x-1)$(x≥2),求函数的导数进行判断即可.
(Ⅱ)求函数的导数,将不等式恒成立进行转化,利用参数分离法进行转化求解即可.
解答 解:(Ⅰ) 解法1:$f'(x)=\frac{{\frac{x-2}{x-1}-ln(x-1)}}{{{{(x-2)}^2}}}$=$\frac{(x-2)-(x-1)ln(x-1)}{{(x-1){{(x-2)}^2}}}$,-----------(2分)
记g(x)=(x-2)-(x-1)ln(x-1)(x>2),g'(x)=-ln(x-1)<0,----------(3分)
即g(x)在(2,+∞)上单调递减,∴g(x)<g(2)=0
从而f'(x)<0,∴函数f(x)在(2,+∞)上的单调递减.----------------------------(5分)
解法2:依题意得$f'(x)=\frac{{\frac{x-2}{x-1}-ln(x-1)}}{{{{(x-2)}^2}}}$,--------------------------------------------(2分)
记$g(x)=\frac{x-2}{x-1}-ln(x-1)$(x≥2)
则$g'(x)=\frac{1}{{{{(x-1)}^2}}}-\frac{1}{x-1}$=$\frac{2-x}{{{{(x-1)}^2}}}$,---------------------------------------------------------(3分)
∵x>2∴g'(x)<0,即函数g(x)在(2,+∞)上单调递减,
∴g(x)<g(2)=0,从而得f'(x)<0,
∴函数f(x)在(2,+∞)上的单调递减.--------------------------------------------------(5分)
(Ⅱ) 解法1:f(x)<a对?x∈(2,+∞)均成立,
等价于ln(x-1)<a(x-2)对?x∈(2,+∞)均成立,-------------------------------------(6分)
由y=ln(x-1)得$y'=\frac{1}{x-1}$,由此可得函数y=ln(x-1)的图象在点(2,0)处的切线
为y=x-2,-----------------------------------------------------------------------------------------(7分)
(1)当a<1时,在(2,+∞)上,直线y=a(x-2)与函数y=ln(x-1)的图象相交,不合题意;---(9分)
(2)当a≥1时,在(2,+∞)上,直线y=a(x-2)在函数y=ln(x-1)的图象的上方,符合题意---------------(11分)
综上得:要使f(x)<a对?x∈(2,+∞)均成立,a∈[1,+∞).------------------------------(12分)
解法2:f(x)<a对?x∈(2,+∞)均成立,
等价于ln(x-1)<a(x-2)对?x∈(2,+∞)均成立---------------------------------------(5分)
记h(x)=ln(x-1)-a(x-2),则$h'(x)=\frac{1}{x-1}-a$=$\frac{1+a-ax}{x-1}$=$\frac{-a}{x-1}(x-\frac{a+1}{a})$-------(6分)h(2)=0,令h'(x)=0得$x=\frac{1+a}{a}$,$\frac{a+1}{a}>2?0<a<1$,
(1)当a≤0时,对?x∈(2,+∞),h'(x)>0,即函数h(x)在(2,+∞)单调递增,
故h(x)>h(2)=0,即ln(x-1)-a(x-2)>0,不符合题意;---------------------------(8分)
(2)当0<a<1时,对$?x∈(2,\frac{1+a}{a})$,h'(x)>0,
此时函数h(x)在$(2,\frac{1+a}{a})$上为增函数,即ln(x-1)-a(x-2)>0,不符合题意;-----(10分)
(3)当a≥1时,对?x∈(2,+∞),有h'(x)<0,函数h(x)在(2,+∞)单调递减,
因此ln(x-1)-a(x-2)<h(2)=0,符合题意;
综上得:要使f(x)<a对?x∈(2,+∞)均成立,a∈[1,+∞).------------------------(12分)
点评 本题主要考查函数单调性的判断以及不等式恒成立问题,求函数的导数,利用参数分离法以及构造法构造新函数,利用导数研究函数的单调性是解决本题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
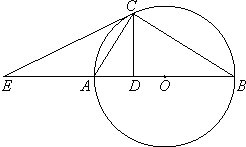 如图,EC切⊙O于点C,直线EO交⊙O于A,B两点,CD⊥AB,垂足为D.
如图,EC切⊙O于点C,直线EO交⊙O于A,B两点,CD⊥AB,垂足为D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
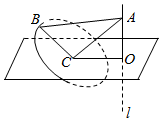 如图所示,已知直线l⊥平面α,垂足O,在△ABC中,BC=1,AC=2,AB=$\sqrt{5}$,若该三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间距离最大值是( )
如图所示,已知直线l⊥平面α,垂足O,在△ABC中,BC=1,AC=2,AB=$\sqrt{5}$,若该三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间距离最大值是( )| A. | 2+$\sqrt{3}$ | B. | 1+$\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于极轴所在直线对称 | B. | 关于极点对称 | ||
| C. | 重合 | D. | 关于直线θ=$\frac{π}{2}$(ρ∈R)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com