
分析 (1)设M及F点坐标,求得向量$\overrightarrow{OM}$和$\overrightarrow{MF}$,根据向量的数量积的坐标表示求得p的值,即可求得抛物线方程;
(2)先根据抛物线方程求得焦点的坐标,进而可求得直线l的方程,代入抛物线方程消去,根据韦达定理及平面向量的数量积运算,可求$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角的余弦值;
(3)由向量数量积的坐标表示,得${y}_{2}^{2}$=λ2${y}_{1}^{2}$,由点A和B在抛物线上,得到B的坐标,根据焦点坐标可得直线的方程,进而求得直线在y轴上的截距,判断g(λ)=$\frac{2\sqrt{λ}}{λ-1}$,在[4,9]上是单调递减,即可l在y轴上截距的变化范围.
解答 解:(1)由题意可知M坐标为($\frac{4}{2p}$,2),F($\frac{p}{2}$,0)
由$\overrightarrow{OM}$=($\frac{4}{2p}$,2),$\overrightarrow{MF}$=($\frac{{p}^{2}-4}{2p}$,-2),
$\overrightarrow{OM}$•$\overrightarrow{MF}$=-4,即$\frac{4}{2p}$×$\frac{{p}^{2}-4}{2p}$-4=-4,解得:p=2,
曲线C的方程y2=4x;
(2)抛物线C的焦点为F(1,0),直线l的斜率为1,
∴l的方程为y=x-1,
将y=x-1代入方程y2=4x整理得:x2-6x+1=0,
由韦达定理可知:x1+x2=6,x1•x2=1,
∴y1+y2=4,y1•y2=-4,
cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{丨\overrightarrow{OA}丨丨\overrightarrow{OB}丨}$=$\frac{{x}_{1}{x}_{2}+{y}_{1}{y}_{2}}{\sqrt{{x}_{1}^{2}+{y}_{1}^{2}}•\sqrt{{x}_{2}^{2}+{y}_{2}^{2}}}$=-$\frac{3\sqrt{41}}{41}$,
$\overrightarrow{OA}$与$\overrightarrow{OB}$夹角的余弦值为-$\frac{3\sqrt{41}}{41}$;
(3)由题设得:(x2-1,y2)=λ(1-x1,-y1),
即x2-1=λ(1-x1),y2=-λy1,
整理得:${y}_{2}^{2}$=λ2${y}_{1}^{2}$,
∵${y}_{1}^{2}$=4x1,${y}_{2}^{2}$=4x2,
∴x2=λ2x1,
∴x2=λ根据题意有λ>0,
∴B(λ,2$\sqrt{λ}$)或B(λ,-2$\sqrt{λ}$),
又F(1,0),
得直线l的方程为(λ-1)y=2$\sqrt{λ}$(x-1)或(λ-1)y=-2$\sqrt{λ}$(x-1),
当λ∈[4,9],时,l在y轴上的截距为$\frac{2\sqrt{λ}}{λ-1}$或-$\frac{2\sqrt{λ}}{λ-1}$,
设g(λ)=$\frac{2\sqrt{λ}}{λ-1}$,λ∈[4,9],
∴g(λ)=$\frac{2\sqrt{λ}}{λ-1}$,在[4,9],上是递减,
∴$\frac{3}{4}$≤$\frac{2\sqrt{λ}}{λ-1}$≤$\frac{4}{3}$或-$\frac{4}{3}$≤-$\frac{2\sqrt{λ}}{λ-1}$≤-$\frac{3}{4}$,
∴直线l在y轴上截距的变化范围为$\frac{3}{4}$≤$\frac{2\sqrt{λ}}{λ-1}$≤$\frac{4}{3}$或-$\frac{4}{3}$≤-$\frac{2\sqrt{λ}}{λ-1}$≤-$\frac{3}{4}$.
点评 本题考查抛物线的标准方程,直线与抛物线的位置关系,一元二次方程根与系数的关系,向量数量积的坐标表示,考查分析问题及解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
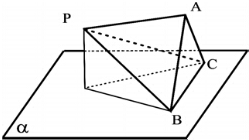 已知正三棱锥P-ABC底面边长为6,底边BC在平面α内,绕BC旋转该三棱锥,若某个时刻它在平面α上的正投影是等腰直角三角形,则此三棱锥高的取值范围是( )
已知正三棱锥P-ABC底面边长为6,底边BC在平面α内,绕BC旋转该三棱锥,若某个时刻它在平面α上的正投影是等腰直角三角形,则此三棱锥高的取值范围是( )| A. | (0,$\sqrt{6}$] | B. | (0,$\frac{\sqrt{6}}{2}$]∪[$\sqrt{6}$,3] | C. | (0,$\frac{\sqrt{6}}{2}$] | D. | (0,$\sqrt{6}$]∪[3,$\frac{3\sqrt{6}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,E是CD的中点,D1E⊥BC.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,E是CD的中点,D1E⊥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com