
分析 根据矩阵的乘法分别求得A2,A3,A4,…,即可求得A10.
解答 解:A2=$[\begin{array}{l}{1}&{1}\\{1}&{1}\end{array}]$$[\begin{array}{l}{1}&{1}\\{1}&{1}\end{array}]$=$[\begin{array}{l}{2}&{2}\\{2}&{2}\end{array}]$,
A3=$[\begin{array}{l}{2}&{2}\\{2}&{2}\end{array}]$$[\begin{array}{l}{1}&{1}\\{1}&{1}\end{array}]$=$[\begin{array}{l}{4}&{4}\\{4}&{4}\end{array}]$=$[\begin{array}{l}{{2}^{2}}&{{2}^{2}}\\{{2}^{2}}&{{2}^{2}}\end{array}]$,
A4=$[\begin{array}{l}{4}&{4}\\{4}&{4}\end{array}]$$[\begin{array}{l}{1}&{1}\\{1}&{1}\end{array}]$=$[\begin{array}{l}{8}&{8}\\{8}&{8}\end{array}]$=$[\begin{array}{l}{{2}^{3}}&{{2}^{3}}\\{{2}^{3}}&{{2}^{3}}\end{array}]$,
…
∴A10=$[\begin{array}{l}{{2}^{9}}&{{2}^{9}}\\{{2}^{9}}&{{2}^{9}}\end{array}]$.
点评 本题考查矩阵的乘法的意义,考查矩阵乘法的运算法则,考查计算能力,属于基础题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
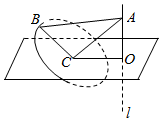 如图所示,已知直线l⊥平面α,垂足O,在△ABC中,BC=1,AC=2,AB=$\sqrt{5}$,若该三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间距离最大值是( )
如图所示,已知直线l⊥平面α,垂足O,在△ABC中,BC=1,AC=2,AB=$\sqrt{5}$,若该三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间距离最大值是( )| A. | 2+$\sqrt{3}$ | B. | 1+$\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
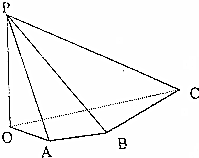 已知四棱锥P一OABC中,PO=3,OA=$\sqrt{7}$,AB=BC=4,PO⊥面OABC,PB⊥BC,且PB与平面OABC所成角为30°,求面APB与面CPB所成二面角的余弦值.
已知四棱锥P一OABC中,PO=3,OA=$\sqrt{7}$,AB=BC=4,PO⊥面OABC,PB⊥BC,且PB与平面OABC所成角为30°,求面APB与面CPB所成二面角的余弦值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com