
分析 (Ⅰ)求出函数的导函数,得到当x>0时,f′(x)<0,当x<0时,f′(x)>0.由此求得f(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减.得到f(x)max=1.又当x→+∞时,f(x)→0,可得函数y=f(x)-a有两个零点的实数a的取值范围为(0,1);
(Ⅱ)g(x)=f(x)-f′(x)e2x=$\frac{x+1}{{e}^{x}}$+xex,求其导函数,可得当x≥0时,g′(x)>0;当x<0时,g′(x)>0.可得g(x)在(-∞,+∞)上单调递增,当x∈[-1,+∞)时,g(x)≥g(-1)=$-\frac{1}{e}$.由$-\frac{1}{e}+b>0$求得实数b的取值范围.
解答 解:(Ⅰ)f(x)=$\frac{x+1}{{e}^{x}}$,f′(x)=$\frac{{e}^{x}-(x+1){e}^{x}}{{e}^{2x}}=\frac{-x}{{e}^{x}}$.
当x>0时,f′(x)<0,当x<0时,f′(x)>0.
∴f(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减.
∴f(x)max=f(0)=1.
又当x→+∞时,f(x)→0,
∴若函数y=f(x)-a有两个零点,则实数a的取值范围为(0,1);
(Ⅱ)g(x)=f(x)-f′(x)e2x=$\frac{x+1}{{e}^{x}}$+xex,
g′(x)=$-\frac{x}{{e}^{x}}+{e}^{x}+x{e}^{x}$=$\frac{x({e}^{2x}-1)}{{e}^{x}}+{e}^{x}$.
当x≥0时,e2x≥1,$\frac{x({e}^{2x}-1)}{{e}^{x}}≥0$,g′(x)>0;
当x<0时,e2x<1,$\frac{x({e}^{2x}-1)}{{e}^{x}}≥0$,g′(x)>0.
∴g(x)在(-∞,+∞)上单调递增,当x∈[-1,+∞)时,g(x)≥g(-1)=$-\frac{1}{e}$.
故只需$-\frac{1}{e}+b>0$,b$>\frac{1}{e}$.
即实数b的取值范围为($\frac{1}{e},+∞$).
点评 本题考查利用导数研究函数的单调性,考查利用导数求函数的极值,训练了恒成立问题的求解方法,体现了分类讨论的数学思想方法,属难题.


科目:高中数学 来源: 题型:解答题
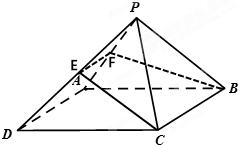 如图,已知在四棱锥P-ABCD中,底面ABCD的边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2,过BC作平面BCEF,交PD于点E,交AP于点F.
如图,已知在四棱锥P-ABCD中,底面ABCD的边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2,过BC作平面BCEF,交PD于点E,交AP于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com