
分析 (Ⅰ)求得f(x)的导数,由导数大于0,可得增区间;导数小于0,可得减区间,进而得到极大值;
(Ⅱ)求出h(x)=a-$\frac{2x}{{e}^{x}}$,令h(x)=0,可得a=$\frac{2x}{{e}^{x}}$,由题意可得x1,x2是方程a=$\frac{2x}{{e}^{x}}$的两根,设g(x)=$\frac{2x}{{e}^{x}}$,求出导数和单调区间、极值和最值,可得a的范围;
(Ⅲ)由(Ⅱ)可得,函数h(x)的两个零点满足0<x1<1<x2,由h(x1)=0aex1=2x1,求出F(x1)的解析式,可得F(x1)在(0,1)上递增,即可得证.
解答 解:(Ⅰ)f(x)=$\frac{x+1}{{e}^{x}}$的导数为f′(x)=$\frac{-x}{{e}^{x}}$,
由f′(x)>0,可得x<0;由f′(x)<0,可得x>0.
即有f(x)在(0,+∞)递减,在(-∞,0)递增.
可得f(x)在x=0处取得极大值,且为1;
(Ⅱ)h(x)=a+2f′(x)=a-$\frac{2x}{{e}^{x}}$,
令h(x)=0,可得a=$\frac{2x}{{e}^{x}}$,
若函数h(x)有两个零点x1,x2,则x1,x2是方程a=$\frac{2x}{{e}^{x}}$的两根,
设g(x)=$\frac{2x}{{e}^{x}}$,g′(x)=$\frac{2-2x}{{e}^{x}}$,
由g′(x)>0,可得x<1,由g′(x)<0,可得x>1,
可得g(x)在(-∞,1)递增,在(1,+∞)递减,
g(x)max=g(1)=$\frac{2}{e}$,
由x→+∞,g(x)→0;x→-∞,g(x)→-∞.
要使方程a=$\frac{2x}{{e}^{x}}$有两根,可得0<a<$\frac{2}{e}$,
故实数a的取值范围是(0,$\frac{2}{e}$);
(Ⅲ)证明:由(Ⅱ)可得,函数h(x)的两个零点满足0<x1<1<x2,
由h(x1)=a-$\frac{2{x}_{1}}{{e}^{{x}_{1}}}$=0,即a=$\frac{2{x}_{1}}{{e}^{{x}_{1}}}$,即aex1=2x1,
由F(x1)=aex1-x12=2x1-x12=-(x1-1)2+1,
显然F(x1)在(0,1)上递增,
由0<x1<1,可得0=F(0)<F(x1)<F(1)=1,
即0<F(x1)<1.
点评 本题考查导数的运用:求单调区间和极值、最值,考查函数方程的转化思想的运用,注意运用构造函数法和函数的单调性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
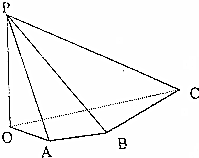 已知四棱锥P一OABC中,PO=3,OA=$\sqrt{7}$,AB=BC=4,PO⊥面OABC,PB⊥BC,且PB与平面OABC所成角为30°,求面APB与面CPB所成二面角的余弦值.
已知四棱锥P一OABC中,PO=3,OA=$\sqrt{7}$,AB=BC=4,PO⊥面OABC,PB⊥BC,且PB与平面OABC所成角为30°,求面APB与面CPB所成二面角的余弦值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
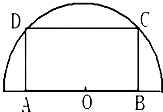 如图,在半径为$10\sqrt{3}(m)$的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),
如图,在半径为$10\sqrt{3}(m)$的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥P-ABCD中,PD⊥底面ABCD,PD=DC=2AD,AD⊥DC,∠BCD=45°.
如图所示,四棱锥P-ABCD中,PD⊥底面ABCD,PD=DC=2AD,AD⊥DC,∠BCD=45°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,△PAB,△PAD,都是边长为2的等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,△PAB,△PAD,都是边长为2的等边三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com