
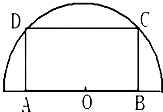
 ��ͼ���ڰ뾶Ϊ$10\sqrt{3}��m��$�İ�Բ�Σ�����OΪԲ�ģ���Ƥ�Ͻ�ȡһ����β���ABCD�����е�C��D��Բ���ϣ���A��B�ڰ�Բ��ֱ���ϣ��ֽ��˾�����ƤABCD����һ����BCΪĸ�ߵ�Բ���ι��ӵIJ��棨ע�����Ƽ��ú�ƴ����ģ�������εı߳�BC=x��m����Բ���IJ����ΪS��m2�������ΪV��m3����
��ͼ���ڰ뾶Ϊ$10\sqrt{3}��m��$�İ�Բ�Σ�����OΪԲ�ģ���Ƥ�Ͻ�ȡһ����β���ABCD�����е�C��D��Բ���ϣ���A��B�ڰ�Բ��ֱ���ϣ��ֽ��˾�����ƤABCD����һ����BCΪĸ�ߵ�Բ���ι��ӵIJ��棨ע�����Ƽ��ú�ƴ����ģ�������εı߳�BC=x��m����Բ���IJ����ΪS��m2�������ΪV��m3�������� ��1������OC����BC��OC���ɵ�OB����Բ������뾶Ϊr����ABΪ����Բ���ܳ����ɵð뾶r������Բ���IJ������ʽ�������ʽ�����ɵõ��������ʽ��
��2�������䷽�Ͷ��κ�������ֵ���ɵò����S�����ֵ��x��ֵ��
��3�������������ĵ������ɵõ�������ͼ�ֵ����Ϊ��ֵ����x��ֵ��
��� 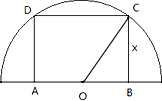 �⣺��1������OC����ΪBC=x��$OC=10\sqrt{3}$��
�⣺��1������OC����ΪBC=x��$OC=10\sqrt{3}$��
����$OB=\sqrt{{{��10\sqrt{3}��}^2}-{x^2}}$������1�֣�
��Բ������뾶Ϊr����$AB=2\sqrt{300-{x^2}}=2��r$��
��$r=\frac{{\sqrt{300-{x^2}}}}{��}$������2�֣�
��$S=2x\sqrt{300-{x^2}}��0��x��10\sqrt{3}��$����4�֣�
$V=��{r^2}x=\frac{{300x-{x^3}}}{��}��0��x��10\sqrt{3}��$����6�֣�
��2��$S=2x\sqrt{300-{x^2}}=2\sqrt{300{x^2}-{x^4}}=2\sqrt{-{{��{x^2}-150��}^2}+22500}��0��x��10\sqrt{3}��$��
���Ե�x2=150ʱ����$x=5\sqrt{6}��m��$ʱ��Բ���IJ����ΪSΪ���10�֣�
��3����$V=��{r^2}x=\frac{{300x-{x^3}}}{��}��0��x��10\sqrt{3}��$
��$V'=\frac{{300-3{x^2}}}{��}$����V'=0���x=10������13�֣�
����x�ʣ�0��10����V'��0����$x�ʣ�10��10\sqrt{3}��$��V'��0��
����$V=\frac{{300x-{x^3}}}{��}$�ڣ�0��10����������������$��10��10\sqrt{3}��$���Ǽ�������
���Ե�x=10��m��ʱ��Բ�������V�����ֵΪ$\frac{2000}{��}��{m^3}��$����16�֣���
���� ���⿼��Բ���IJ�������������ֵ����ע�����ö��κ�������ֵ���ɵ��������䡢��ֵ����ֵ�����黯�����������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
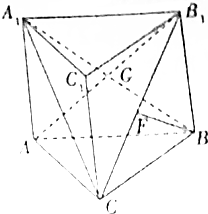 ��ͼ��ʾ����������ABC-A1B1C1�У�����ABB1A1�ĶԽ����ཻ�ڵ�G���Ҳ���ABB1A1��ƽ��ABC��AC=CB=BB1=2��FΪCB1�ϵĵ㣬��BF��ƽ��AB1C��
��ͼ��ʾ����������ABC-A1B1C1�У�����ABB1A1�ĶԽ����ཻ�ڵ�G���Ҳ���ABB1A1��ƽ��ABC��AC=CB=BB1=2��FΪCB1�ϵĵ㣬��BF��ƽ��AB1C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{6}$ | B�� | $\sqrt{3}$ | C�� | $\sqrt{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪AB��AC��Բ�������ң���B��Բ��������AC���ӳ����ཻ��D������C��BD��ƽ������AB�ཻ�ڵ�E��AE=3��BE=1����BC�ij�Ϊ��������
��ͼ����֪AB��AC��Բ�������ң���B��Բ��������AC���ӳ����ཻ��D������C��BD��ƽ������AB�ཻ�ڵ�E��AE=3��BE=1����BC�ij�Ϊ��������| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 2 | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com