
| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
分析 利用${V}_{{D}_{1}-AE{C}_{1}}$=${V}_{A-E{C}_{1}{D}_{1}}$,即可求出点D1到平面AEC1的距离.
解答  解:设点D1到平面AEC1的距离为h.
解:设点D1到平面AEC1的距离为h.
如图所示△AEC1中,AE=EC1=$\frac{3\sqrt{5}}{2}$,AC1=3$\sqrt{3}$,
∴${S}_{△AE{C}_{1}}$=$\frac{1}{2}×3\sqrt{3}×\sqrt{(\frac{3\sqrt{5}}{2})^{2}-(\frac{3\sqrt{3}}{2})^{2}}$=$\frac{9\sqrt{6}}{4}$,
∵${V}_{{D}_{1}-AE{C}_{1}}$=${V}_{A-E{C}_{1}{D}_{1}}$,
∴$\frac{1}{3}×\frac{9\sqrt{6}}{4}h=\frac{1}{3}×\frac{1}{2}×3×3×3$,
∴h=$\sqrt{6}$,
∴点D1到平面AEC1的距离为$\sqrt{6}$,
故选:A.
点评 本题以正方体为载体,考查了立体几何中点、线、面的距离的计算,属于中档题.运用体积计算公式,进行等体积转换来求点到平面的距离,是解决本题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
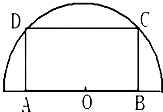 如图,在半径为$10\sqrt{3}(m)$的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),
如图,在半径为$10\sqrt{3}(m)$的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
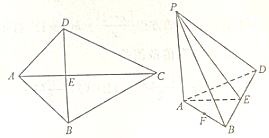 如图,AC为线段BD的垂直平分线,且AE=BE=$\frac{1}{2}$CE=1,现将△BCD沿线段BD翻折到PBD,使二面角P-BD-A为60°.
如图,AC为线段BD的垂直平分线,且AE=BE=$\frac{1}{2}$CE=1,现将△BCD沿线段BD翻折到PBD,使二面角P-BD-A为60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,△PAB,△PAD,都是边长为2的等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,△PAB,△PAD,都是边长为2的等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com