
分析 (Ⅰ)由题意利用斜率公式可得函数f(x)的解析式,求出导函数分别由导函数大于0和小于0求出原函数的单调区间,进一步求得极值;
(Ⅱ)把f(x)的解析式代入g(x)=$\frac{x}{a(1-x)}$[xf(x)-1],分析可知,若a<0,当x∈(0,1)时,f(x)>0与题意不符.可得a>0.由g(x)>-1,得$\frac{xlnx}{a(1-x)}>-1⇒lnx+\frac{a(1-x)}{x}>0$,构造函数$h(x)=lnx+\frac{a(1-x)}{x}=lnx+\frac{a}{x}-a,x∈(0,1)$,求其导函数,然后对a分类分析得答案.
解答 解:(Ⅰ)依题意,P(x,1+lnx),则$f(x)=\frac{1+lnx}{x}$,x>0,
于是,$f'(x)=-\frac{lnx}{x^2}$,
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
故f(x)在x=1处取得极大值,且极大值为f(1)=1;无极小值.
(Ⅱ)$g(x)=\frac{x}{a(1-x)}[{xf(x)-1}]=\frac{xlnx}{a(1-x)}$,
可知,若a<0,∵x∈(0,1),∴f(x)>0与题意不符.则a>0.
由g(x)>-1,得$\frac{xlnx}{a(1-x)}>-1⇒lnx+\frac{a(1-x)}{x}>0$,
记$h(x)=lnx+\frac{a(1-x)}{x}=lnx+\frac{a}{x}-a,x∈(0,1)$,$h'(x)=\frac{1}{x}-\frac{a}{x^2}=\frac{x-a}{x^2}$.
①若a≥1,则h'(x)<0恒成立,从而h(x)在(0,1)上递减,h(x)>h(1)=0,满足题意;
②若0<a<1,则当x∈(0,a)时,h'(x)<0;x∈(a,1)时,h'(x)>0,
∴h(x)在(0,a)上递减,在(a,1)上递增.
∴x∈(a,1)时,h(x)<h(1)=0,不满足题意.
综上,a的取值范围是[1,+∞).
点评 本题考查利用导数研究函数的单调性,考查利用导数求函数的极值,训练了恒成立问题的求解方法,体现了分类讨论的数学思想方法,属难题.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:填空题
 如图,直线l⊥平面α,垂足为O,正四面体(所有棱长都相等的三棱锥)ABCD的棱长为a,C在平面α内,B是直线l上的动点,当点O到AD的距离最大时,直线AD与平面α的距离为$\frac{2+\sqrt{2}}{4}$a.
如图,直线l⊥平面α,垂足为O,正四面体(所有棱长都相等的三棱锥)ABCD的棱长为a,C在平面α内,B是直线l上的动点,当点O到AD的距离最大时,直线AD与平面α的距离为$\frac{2+\sqrt{2}}{4}$a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
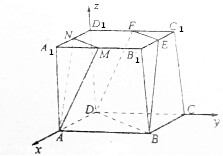 如图,正方体ABCD-A1B1C1D1的棱长为a,点M、N、E、F分别是A1B1、A1D1、B1C1、C1D1的中点,则点M到平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;直线AM与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;平面AMN与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$.
如图,正方体ABCD-A1B1C1D1的棱长为a,点M、N、E、F分别是A1B1、A1D1、B1C1、C1D1的中点,则点M到平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;直线AM与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;平面AMN与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
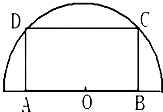 如图,在半径为$10\sqrt{3}(m)$的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),
如图,在半径为$10\sqrt{3}(m)$的半圆形(其中O为圆心)铝皮上截取一块矩形材料ABCD,其中点C、D在圆弧上,点A、B在半圆的直径上,现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面(注:不计剪裁和拼接损耗),设矩形的边长BC=x(m),圆柱的侧面积为S(m2)、体积为V(m3),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com