
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
分析 可画出图形,根据向量加法的平行四边形法则及向量的数乘运算便可得出$\overrightarrow{GA}=-\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$,$\overrightarrow{GB}=-\frac{1}{3}(-2\overrightarrow{AB}+\overrightarrow{AC})$,$\overrightarrow{GC}=-\frac{1}{3}(\overrightarrow{AB}-2\overrightarrow{AC})$,这样带入$a\overrightarrow{GA}+b\overrightarrow{GB}+c\overrightarrow{GC}=\overrightarrow{0}$并进行向量的数乘运算整理可得到$(-\frac{1}{3}a+\frac{2}{3}b-\frac{1}{3}c)\overrightarrow{AB}+(-\frac{1}{3}a-\frac{1}{3}b+\frac{2}{3}c)$$\overrightarrow{AC}=\overrightarrow{0}$,从而便可得出$\left\{\begin{array}{l}{-\frac{1}{3}a+\frac{2}{3}b-\frac{1}{3}c=0}\\{-\frac{1}{3}a-\frac{1}{3}b+\frac{2}{3}c=0}\end{array}\right.$,进行整理便可得出a=b=c,从而便可得出角C的大小.
解答 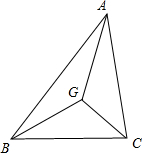 解:如图,
解:如图,
根据条件,$\overrightarrow{GA}=-\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$,$\overrightarrow{GB}=-\frac{1}{3}(\overrightarrow{BA}+\overrightarrow{BC})=-\frac{1}{3}(-2\overrightarrow{AB}+\overrightarrow{AC})$,$\overrightarrow{GC}=-\frac{1}{3}(\overrightarrow{CB}+\overrightarrow{CA})=-\frac{1}{3}(\overrightarrow{AB}-2\overrightarrow{AC})$;
又$a\overrightarrow{GA}+b\overrightarrow{GB}+c\overrightarrow{GC}=\overrightarrow{0}$;
∴$-\frac{1}{3}a(\overrightarrow{AB}+\overrightarrow{AC})-\frac{1}{3}b(-2\overrightarrow{AB}+\overrightarrow{AC})$$-\frac{1}{3}c(\overrightarrow{AB}-2\overrightarrow{AC})$=$(-\frac{1}{3}a+\frac{2}{3}b-\frac{1}{3}c)\overrightarrow{AB}$$+(-\frac{1}{3}a-\frac{1}{3}b+\frac{2}{3}c)\overrightarrow{AC}=\overrightarrow{0}$;
∴$\left\{\begin{array}{l}{-\frac{1}{3}a+\frac{2}{3}b-\frac{1}{3}c=0}\\{-\frac{1}{3}a-\frac{1}{3}b+\frac{2}{3}c=0}\end{array}\right.$;
整理得a=b=c;
∴△ABC为等边三角形,则:C=60°.
故选C.
点评 考查三角形重心的概念及性质,向量加法的平行四边形法则,以及向量数乘的几何意义及向量的数乘运算,平面向量基本定理.


 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:填空题
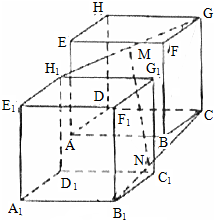 将棱长为1的正方体ABCD-EFGH任意平移至A1B1C1D1-E1F1G1H1,连接GH1,CB1,设M,N分别为GH1,CB1的中点,则MN的长为$\frac{\sqrt{6}}{2}$.
将棱长为1的正方体ABCD-EFGH任意平移至A1B1C1D1-E1F1G1H1,连接GH1,CB1,设M,N分别为GH1,CB1的中点,则MN的长为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 人如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,∠BAD=60°,AB=2AD,AP⊥BD.
人如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,∠BAD=60°,AB=2AD,AP⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
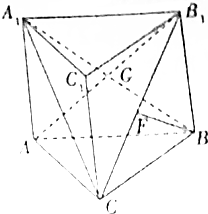 如图所示,在三棱柱ABC-A1B1C1中,矩形ABB1A1的对角线相交于点G,且侧面ABB1A1⊥平面ABC,AC=CB=BB1=2,F为CB1上的点,且BF⊥平面AB1C.
如图所示,在三棱柱ABC-A1B1C1中,矩形ABB1A1的对角线相交于点G,且侧面ABB1A1⊥平面ABC,AC=CB=BB1=2,F为CB1上的点,且BF⊥平面AB1C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com