
分析 根据题意,分析可得人数分配上有两种方式即1,2,2与1,1,3,分别计算两种情况下的情况数目,相加可得答案.
解答 解:人数分配上有两种方式即1,2,2与1,1,3.
若是1,1,3,则有$\frac{{C}_{5}^{3}{•C}_{2}^{1}}{{A}_{2}^{2}}$•A${\;}_{3}^{3}$=10×6=60种;
若是1,2,2,则有$\frac{{C}_{5}^{1}{•C}_{4}^{2}{•C}_{2}^{2}}{{A}_{2}^{2}}$•A${\;}_{3}^{3}$=15×6=90种.
所以共有60+90=150种不同的方法.
故答案为:150.
点评 本题考查排列、组合的应用题的解法,注意先分组再全排,正确分类是解题的关键,属于中档题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D是PC的中点.
如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
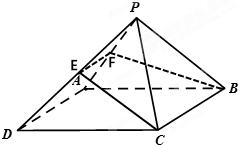 如图,已知在四棱锥P-ABCD中,底面ABCD的边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2,过BC作平面BCEF,交PD于点E,交AP于点F.
如图,已知在四棱锥P-ABCD中,底面ABCD的边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2,过BC作平面BCEF,交PD于点E,交AP于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
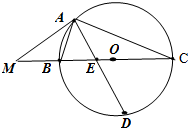 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点M,∠BAC的平分线分别交圆O和BC于点D,E,若MA=$\frac{5}{2}$MB=15.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点M,∠BAC的平分线分别交圆O和BC于点D,E,若MA=$\frac{5}{2}$MB=15.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
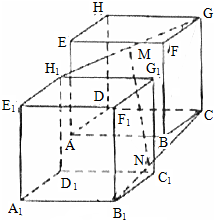 将棱长为1的正方体ABCD-EFGH任意平移至A1B1C1D1-E1F1G1H1,连接GH1,CB1,设M,N分别为GH1,CB1的中点,则MN的长为$\frac{\sqrt{6}}{2}$.
将棱长为1的正方体ABCD-EFGH任意平移至A1B1C1D1-E1F1G1H1,连接GH1,CB1,设M,N分别为GH1,CB1的中点,则MN的长为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com