
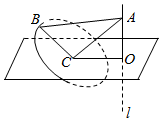
 如图所示,已知直线l⊥平面α,垂足O,在△ABC中,BC=1,AC=2,AB=$\sqrt{5}$,若该三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间距离最大值是( )
如图所示,已知直线l⊥平面α,垂足O,在△ABC中,BC=1,AC=2,AB=$\sqrt{5}$,若该三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间距离最大值是( )| A. | 2+$\sqrt{3}$ | B. | 1+$\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
分析 先将原问题转化为平面内的最大距离问题解决,以O为原点,OA为y轴,OC为x轴建立直角坐标系,B、O两点间的距离表示处理,结合三角函数的性质求出其最大值即可.
解答 解:将原问题转化为平面内的最大距离问题解决,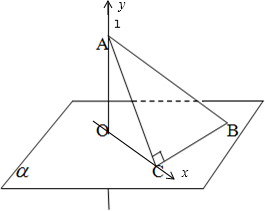
以O为原点,OA为y轴,OC为x轴建立直角坐标系,如图.
设∠ACO=θ,B(x,y),则有:x=ACcosθ+BCsinθ=2cosθ+
sinθ,y=BCcosθ=cosθ.
∴x2+y2=4cos2θ+4sinθcosθ+1=2cos2θ+2sin2θ+3
=2$\sqrt{2}$sin(2θ+$\frac{π}{4}$)+3,
当sin(2θ+$\frac{π}{4}$)=1时,x2+y2最大,为2$\sqrt{2}$+3,
则B、O两点间的最大距离为1+$\sqrt{2}$.
故选:B.
点评 本题考查了点、线、面间的距离计算,解答关键是将空间几何问题转化为平面几何问题解决,利用三角函数的知识求最大值.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
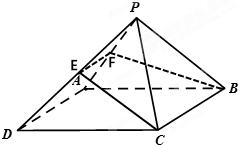 如图,已知在四棱锥P-ABCD中,底面ABCD的边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2,过BC作平面BCEF,交PD于点E,交AP于点F.
如图,已知在四棱锥P-ABCD中,底面ABCD的边长为2的菱形,∠BCD=120°,AP=BP,∠APB=90°,PC=2,过BC作平面BCEF,交PD于点E,交AP于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
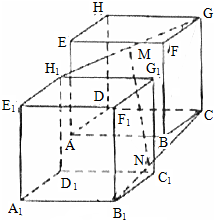 将棱长为1的正方体ABCD-EFGH任意平移至A1B1C1D1-E1F1G1H1,连接GH1,CB1,设M,N分别为GH1,CB1的中点,则MN的长为$\frac{\sqrt{6}}{2}$.
将棱长为1的正方体ABCD-EFGH任意平移至A1B1C1D1-E1F1G1H1,连接GH1,CB1,设M,N分别为GH1,CB1的中点,则MN的长为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com