
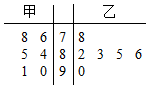
 吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示:
吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示:分析 (1)由茎叶图分别求出$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,${{S}_{甲}}^{2}$,${{S}_{乙}}^{2}$,由$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${{S}_{甲}}^{2}>{{S}_{乙}}^{2}$,得到乙学生参加更合适.
(2)由已知得ξ取值为0,1,2,3,4,且ξ~B(4,$\frac{1}{3}$),由此能求出ξ的分布列和Eξ.
解答 解:(1)由茎叶图得:
$\overline{{x}_{甲}}$=$\frac{76+78+84+85+90+91}{6}$=84,
$\overline{{x}_{乙}}$=$\frac{78+82+83+85+86+90}{6}$=84,
${{S}_{甲}}^{2}$=$\frac{1}{6}$[(76-84)2+(78-84)2+(84-84)2+(85-84)2+(90-84)2+(91-84)2]=31,
${{S}_{乙}}^{2}$=$\frac{1}{6}$[(78-84)2+(82-84)2+(83-84)2+(85-84)2+(86-84)2+(90-84)2]=$\frac{41}{6}$,
$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,${{S}_{甲}}^{2}>{{S}_{乙}}^{2}$,
∴乙学生参加更合适.
(2)不少于86分的频率为$\frac{1}{3}$,故每次成绩不少于86分的概率p=$\frac{1}{3}$,
ξ取值为0,1,2,3,4,且ξ~B(4,$\frac{1}{3}$),
P(ξ=0)=${C}_{4}^{0}(\frac{1}{3})^{0}(\frac{2}{3})^{4}$=$\frac{16}{81}$,
P(ξ=1)=${C}_{4}^{1}(\frac{1}{3})(\frac{2}{3})^{3}$=$\frac{32}{81}$,
P(ξ=2)=${C}_{4}^{2}(\frac{1}{3})^{2}(\frac{2}{3})^{2}$=$\frac{24}{81}$,
P(ξ=3)=${C}_{4}^{3}(\frac{1}{3})^{3}(\frac{2}{3})$=$\frac{8}{81}$,
P(ξ=4)=${C}_{4}^{4}(\frac{1}{3})^{4}(\frac{2}{3})^{0}$=$\frac{1}{81}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{16}{81}$ | $\frac{32}{81}$ | $\frac{24}{81}$ | $\frac{8}{81}$ | $\frac{1}{81}$ |
点评 本题考查茎叶图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:选择题
| 第x天 | 1 | 2 | 3 | 4 | 5 |
| 被感染的计算机数量y(台) | 12 | 24 | 49 | 95 | 190 |
| A. | y=12x | B. | y=6x2-6x+12 | C. | y=6•2x | D. | y=12log2x+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
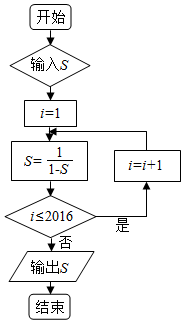
| A. | -1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4$\sqrt{2}$,+∞) | B. | [3$\sqrt{2}$,+∞) | C. | [2$\sqrt{2}$,+∞) | D. | [$\frac{5}{2}$$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分 组(分数段) | 频 数(人 数) | 频 率 |
| [60,70) | 8 | |
| [70,80) | 0.44 | |
| [80,90) | 14 | 0.28 |
| [90,100 | ||
| 合 计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com