
| 分 组(分数段) | 频 数(人 数) | 频 率 |
| [60,70) | 8 | |
| [70,80) | 0.44 | |
| [80,90) | 14 | 0.28 |
| [90,100 | ||
| 合 计 | 50 | 1 |
分析 (Ⅰ)由频率=$\frac{频数}{总数}$,能完成频率分布表.
(Ⅱ)①该同学答满5道题并获一等奖,即前4道题回答结果对错,而第5道题答对,由此能求出该同学恰好答满5道题并获一等奖的概率.
②该同学答题的个数可能为3、4、5,即X的可能取值为3、4、5,分另求出相应的概率,由此能求出X的分布列和数学期望.
解答 (本小题满分13分)
解:(Ⅰ)由频率=$\frac{频数}{总数}$,得频率分布表为:
| 分 组(分数段) | 频 数(人 数) | 频 率 |
| [60,70) | 8 | 0.16 |
| [70,80) | 22 | 0.44 |
| [80,90) | 14 | 0.28 |
| [90,100[来源:.Com | 6 | 0.12 |
| 合 计 | 50 | 1 |
| X | 3 | 4 | 5 |
| P | $\frac{1}{4}$ | $\frac{3}{8}$ | $\frac{3}{8}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰发生k次的概率计算公式的合理运用.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,8) | B. | (-∞,-2)∪(8,+∞) | C. | (-4,16) | D. | (-∞,-4)∪(16,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
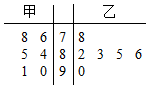 吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示:
吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$-i | B. | -$\sqrt{3}$+i | C. | 1+$\sqrt{3}$i | D. | 1-$\sqrt{3}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com